
法人税や事業税、消費税などの中間納付額を計算する際、端数処理の関係上、きれいに前期の確定年税額の半分にならないことがあります。
例えば、前期(期間は12か月)の確定年税額が500,000円の場合、当期の中間納付額(6か月分)は、税法の規定に従って計算すると次のようになります。
500,000円×6/12=249,900円
数学的に考えたらあり得ない数式で、「小学生からやり直せ!」と言われてしまいそうですが、税法上はこのように計算するのです。
さて、今回の記事の本題は、「中間納付額の計算過程においてどのタイミングで端数処理を行うべきか?」についてです。
実は、実務書や各資格学校のテキストなどを見ても、中間納付額の計算過程における端数処理をどのタイミングで行うかについては見解がバラバラなのです。
具体的には、「月数で除したタイミングで端数処理をする派」と「月数で除した時点では端数処理せず、6(又は3)をかけた後の最後のタイミングで端数処理をする派」の2大派閥に分かれています。
両方の計算方法を見たことがある方にとっては「どっちが正しいの?」と疑問に感じるところだと思います。
そこで今回は、中間納付額を計算する際の円未満切捨の端数処理のタイミングはいつなのかについて解説したいと思います。
端数処理の方法は国税通則法に規定されている
中間納付額について計算する前に、まずは税法上の税額の計算方法の前提条件について見てみましょう。
税金の額を計算する際の端数処理の方法は、国税通則法に規定されています。
① 計算過程で生じた端数は1円未満切捨て
国税通則法第119条において、税金の計算過程における算出額に1円未満の端数があるときは、その端数金額は切り捨てることとされています。
(国税の確定金額を算出する過程における算出額の端数計算)
6 国税の確定金額を算出する過程におけるその算出額に、1円未満の端数があるときは、その端数金額を切り捨てるものとする。
② 税金の確定金額は100円未満切捨て
また、国税通則法119条において、税金の確定金額に100円未満の端数があるときは、その100円未満の端数を切り捨てることとされています。
(国税の確定金額の端数計算等)
第百十九条 国税(自動車重量税、印紙税及び附帯税を除く。以下この条において同じ。)の確定金額に百円未満の端数があるとき、又はその全額が百円未満であるときは、その端数金額又はその全額を切り捨てる。
「これ」という文言の解釈により端数処理のタイミングは異なる
中間納付額の計算方法については、国税通則法ではなく法人税法や消費税法など、各税目ごとに別々に規定されています。
例えば、法人税の中間申告に関する条文では、中間納付額の計算方法について次のように規定しています。
一 当該事業年度の前事業年度の確定申告書に記載すべき第七十四条第一項第二号(確定申告)に掲げる金額で当該事業年度開始の日以後六月を経過した日の前日までに確定したものを当該前事業年度の月数で除し、これに六を乗じて計算した金額(略)
また、消費税の三月中間申告に関する条文では、中間納付額の計算方法について次のように規定しています。
一 当該課税期間の直前の課税期間の確定申告書に記載すべき第四十五条第一項第四号に掲げる消費税額で当該三月中間申告対象期間の末日までに確定したものを当該直前の課税期間の月数で除し、これに三を乗じて計算した金額
このように、どの税目の条文でも似たような表現がされており、「『これ』に○を乗じて~」という表現になっているものが多いです。
さて、上記の赤字で示した「これ」とは、一体どう解釈したらよいのでしょうか?
例えば、前期の税額が500,000円で、前期の月数が12か月、当期の中間申告分の期間が6か月の場合は、500,000円を12で除したものが「これ」になります。
この「これ」については「金額」と考えればいいのか、「比率」と考えればいいのか、どちらでしょうか?
実は、「これ」が指すのが「金額」であるか「比率」であるかの明確な規定はなく、読む人によって解釈の仕方はそれぞれ異なります。
また、「これ」の解釈の仕方によって、中間納付額を計算する際の端数処理のタイミングが変わってきます。
「これ」を「金額」と解釈する場合
国税通則法第119条において、税金の計算過程における算出額に1円未満の端数があるときは、その端数金額は切り捨てることとされています。
したがって、中間納付額の条文中の「これ」を「金額」であると解釈する場合は、国税通則法の規定に従い、前期確定年税額を月数で割った時点で円未満の端数を切り捨てます。
例えば、前期の税額が500,000円で、前期の月数が12か月、当期の中間申告分の期間が6か月の場合は、次のように計算します。
① 500,000 ÷ 12 = 41,666.6666… → 41,666(円未満切捨)←金額なので端数処理する
② 41,666 × 6 =249,996 → 249,900(百円未満切捨)
「これ」を「比率」と解釈する場合
中間納付額の条文中の「これ」を「比率」であると解釈する場合は、「計算過程における算出『額』」ではないため、前期確定年税額を月数で割った時点では1円未満切捨ての端数処理は行いません。
したがって、前期の税額が500,000円で、前期の月数が12か月、当期の中間申告分の期間が6か月の場合は、次のように計算します。
① 500,000 ÷ 12 = 41,666.6666… ← 金額ではなく比率なので端数処理しない
② 41,666.6666… × 6 =249,999.9999… → 249,900(百円未満切捨)
数学的には「0.9999…=1」となりますが、税法上は小数点以下の「.9999…」は「円未満の端数」であるため、国税通則法の規定により切り捨てることとなります。
どちらの方法でも必ず同じ金額になるため気にしなくてよい
「どっちが正しいの?」と疑問に思われた方も多いかと思いますが、実は「どっちでもいい」のです。
どちらの方法で計算しても最終的な金額は必ず同じになるため、気にしなくても大丈夫です。
どっちでも同じ金額になることの証明
「どっちでもいいと言われても、いまいち納得できない!本当にどんな場合でも同じ金額になるの?」と疑問に感じる方もいるかと思います。(自分がそうでした。)
そこで、どちらの方法で計算しても最終的な金額が同じになるということについて、数学的に証明したいと思います。
前事業年度(又は前課税期間)の確定税額をx円、前事業年度(又は前課税期間)の月数をmか月、中間申告対象期間をnか月とします。
このとき、国税通則法の規定により確定税額は100円未満切捨てするためxは100の倍数の正の整数、mとnはそれぞれ1≦m≦12、1≦n≦6を満たす整数となります。
xが100mで割り切れる場合
まず、前事業年度の確定税額x円が、前事業年度(又は前課税期間)の月数の100倍である100mで割り切れる場合について考えます。
このとき、xを100mで割った商をT(Tは整数)とした場合、x/mは次のように表せます。

「これ」を「金額」と捉えた場合の中間納付額
条文中の「これ」を「金額」と捉えた場合は、前事業年度の確定税額x円を前事業年度(又は前課税期間)の月数mで割った(x/m)について円未満切捨ての端数処理を行います。
(x/m)の端数処理を行った金額は、「ガウス記号」を用いて、次のように表すことができます。
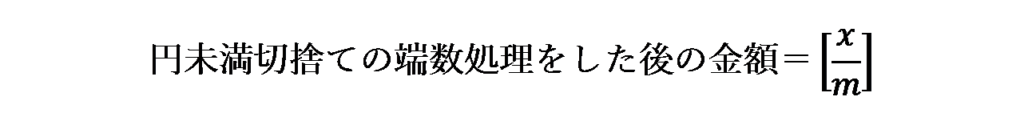
ガウス記号とは、以下のような性質を持つ関数で、床関数、フロアー関数、整数部分などと呼ばれることもあります。
ガウス記号
[ ]で表される関数。ある値を越えない最大の整数値を表す。X を実数,n を整数としたとき、n ≦ X < n+1 ならば,[X]=n である。例えば,[2.34]=2,[-3.54]=-4。
また、中間納付額はxをmで割って端数処理した後の金額[x/m]にnを掛けて、百円未満切捨てした金額であるため、[x/m]×nを100で割ってから円未満切捨て(ガウス記号をつける)し、その後100を掛ければ数式で中間納付額を表すことができます。
したがって、「これ」を「金額」と捉えた場合の中間納付額は次のように表せます。
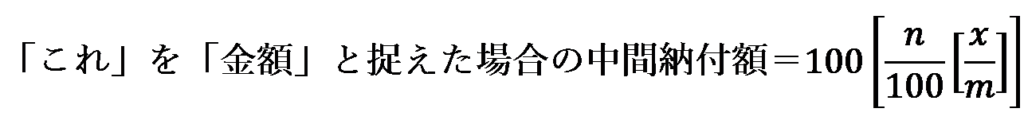
この数式に、x/m=100Tを代入すると、次のようになります。100TもnTも整数値であるため、ガウス記号を外すことができます。

「これ」を「比率」と捉えた場合の中間納付額
条文中の「これ」を「比率」と捉えた場合は、前事業年度の確定税額x円を前事業年度(又は前課税期間)の月数mで割った(x/m)について端数処理は行わず、中間申告対象期間nを乗じたタイミングで百円未満切捨てをして税額を求めます。
この場合の中間納付額は、次のように表すことができます。
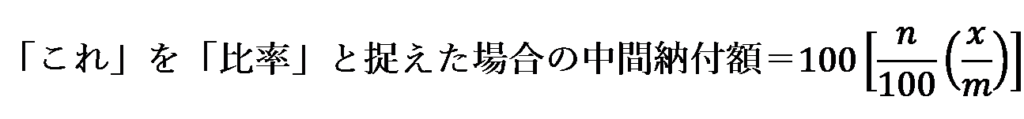
この数式に、x/m=100Tを代入すると、次のようになります。

結論
以上より、xが100mで割り切れる場合は
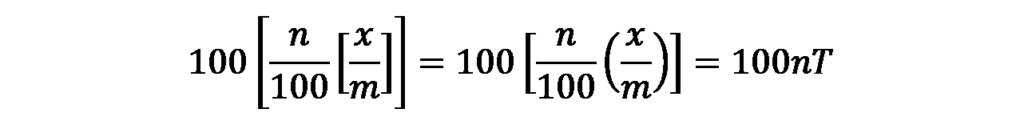
とるため、条文中の「これ」を「金額」と捉えたとしても「比率」と捉えたとしても必ず同じ金額になることがわかりました。
xが100mで割り切れない場合
まず、前事業年度の確定税額x円が、前事業年度(又は前課税期間)の月数の100倍である100mで割り切れない場合について考えます。
この場合、xを100mで割った商をp、xを100mで割った余りをさらにmで割った商をq、xを100mで割った余りをさらにmで割った余りをrとして、xを次のように表します。
![]()
このとき、p、q、rはそれぞれ正の整数で、rはmの剰余であるためr<mとなります。
これを踏まえて、「これ」を「金額」と捉えた場合と「比率」と捉えた場合のそれぞれの場合について考えてみましょう。
「これ」を「金額」と捉えた場合の中間納付額
条文中の「これ」を「金額」と捉えた場合の中間納付額は、xが100mで割り切れる場合と同様に次の数式で表すことができます。
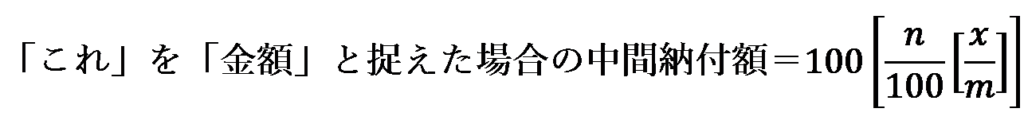
この数式に、x=100mp+mq+rを代入すると、次のようになります。
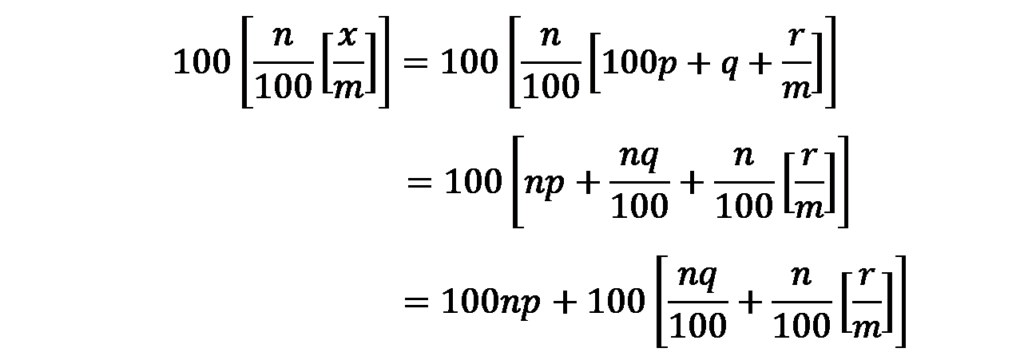
ここで、rはmで割った余りであるため、必ずr<mとなることから、次のことがいえます。
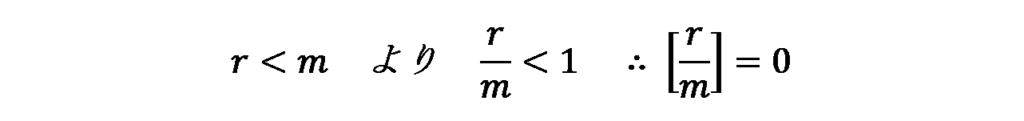
したがって、この場合の中間納付額は次のように表すことができます。
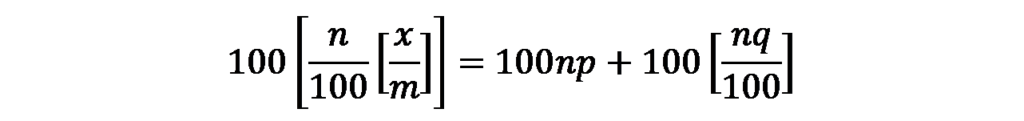
「これ」を「比率」と捉えた場合の中間納付額
条文中の「これ」を「比率」と捉えた場合は、少し工夫が必要になります。
数学的には、小数点のあとに9が続く無限小数は1と等しくなりますが、税法上の計算では、小数点のあとに9が無限に続く場合であっても小数点以下の端数は切り捨てて計算することになるため、数学上の計算結果と税務上の計算結果が異なることがあります。
そこで、数学上の計算結果と税務上の計算結果を一致させるために、とても小さい任意の実数ε(イプシロン)を用いて、中間納付額を以下のように表します。
-1024x121.png)
例えば、ε=0.000000001として、前期の税額が500,000円で、前期の月数が12か月、当期の中間申告分の期間が6か月の場合の中間納付額を上記数式に当てはめて計算すると、

となり、税務上の計算結果と一致することになります。
この数式に、x=100mp+mq+rを代入すると、次のようになります。
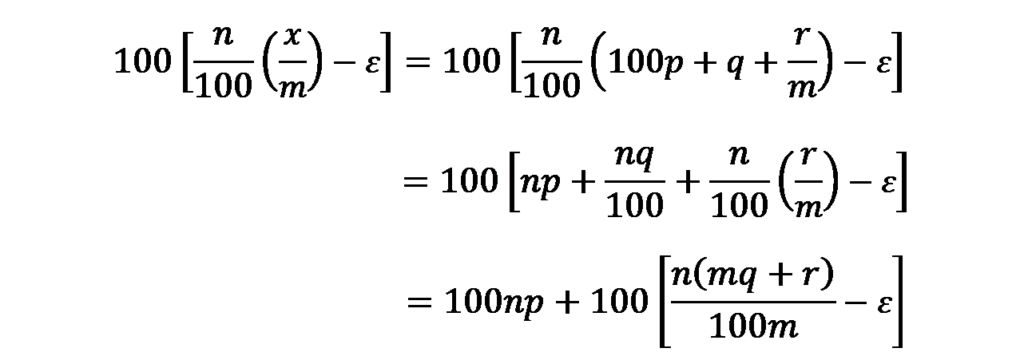
ここで、(mq+r)は、Xを100mで割った余りですが、これにnを乗じたn(mq+r)は100mの公倍数となる可能性があります。
しかし、計算式ではεをマイナスしているため、計算式のガウス記号の中が整数値になることはありません。
また、n<100、r<mであり、(mq+r)は100mの剰余なので、nq/100の整数部分がn(mq+r)/100mより小さい最大の整数となります。
したがって、この場合の中間納付額は次のように表すことができます。
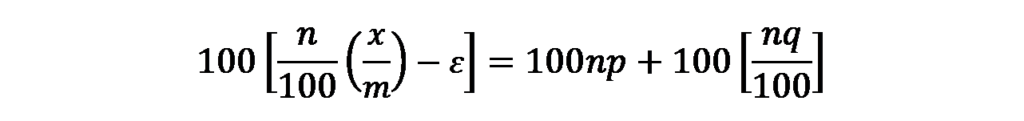
結論
以上より、xが100mで割り切れない場合についても
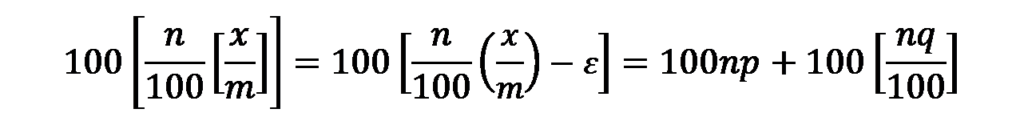
となるため、条文中の「これ」を「金額」と捉えたとしても「比率」と捉えたとしても必ず同じ金額になることがわかりました。
∴どんな場合であっても計算結果は同じになる
以上より、中間納付額の計算はどのタイミングで端数処理を行ったとしても必ず同じ金額になることが証明できました。
まとめ
中間納付額の計算方法は、条文の解釈の違いにより、前期確定年税額を月数で除したタイミングで端数処理を行う方法と、月数で除してさらに当期の中間申告対象期間の月数で乗じたタイミングで端数処理する方法の2種類があり、実務書や資格学校のテキストなどでも計算方法はバラバラで統一されていません。(僕がいくつか調べた限りでは「前期確定年税額を月数で除したタイミングで端数処理を行う方法」の方が多数派のようでした。)
しかし、端数処理のタイミングは上記いずれの方法であっても必ず同じ金額になるため、実務的には全く気にする必要はありません。
税理士試験などの試験で中間納付額の計算過程を書く場合も、端数処理が行われるタイミングに配点が置かれる可能性は低いと考えられるため、そこまで神経質になる必要はないと思います。
(なお、住民税の予定納税額の計算では、そもそも「割ってから掛ける」のではなく「掛けてから割る」ことになるため、端数処理のタイミングに違いが生じることはありません。)














-端っこカット小-1.jpg)
はじっこカット小-1.jpg)
-はじっこカット小-1.jpg)

はじっこカット小.jpg)
-端っこカット小.jpg)
はじっこカット.jpg)
-はじっこカット小.jpg)


