令和３年４月１日から商品価格の総額表示が義務化されたことにより、原則としてすべての商品が税込価格で表示されるようになりました。
そこで、突然ですが皆さん、税込1,000円（消費税率10％）の商品を購入した場合、消費税額はいくらになるかご存知ですか？
お昼ご飯に定食屋で税込1,000円のとんかつ定食を食べて、お腹もいっぱいになったし、消費税もしっかり納税して国民の三大義務の一つを果たしたと満足した気になっているそこのあなた、その1,000円のうちいくらを消費税として支払ったのかちゃんと把握していますか？
「え？1,000円を1.1で割ったら909.09…円になるから、90円か91円…？」と、戸惑いながら答えているあなた、チコちゃんに「ボーっと生きてんじゃねーよ！」と叱られてしまいますよ。
今回は、税込1,000円の商品に含まれる消費税額・本体価格の計算を例に、数学的に消費税額・本体価格が整数値として存在しないことになる税込金額があるということについて及びそのような税込価格の商品の価格表示の方法について解説したいと思います。
消費税額の計算方法
商品価格の内訳として表示する消費税額の計算方法には、以下の３種類の方法があります。
商品価格の内訳として表示する消費税額は、その金額がそのまま税務署への納付税額になるわけではなく、あくまでも消費者に対して商品価格のうち消費税額がいくらぐらいなのかを示すためのものです。
したがって、どの方法で計算するかは法律等で特に決まっておらず、商品を販売する事業者の選択に委ねられています。
実際のところ、多くの事業者が①小数点未満切捨の方法により消費税の表示額を計算しているため、この記事では消費税額の計算はすべて税抜本体価格に消費税率を乗じて小数点未満切捨して求めるという前提で話を進めていきます。
例えば、税抜本体価格532円の商品（税率10％）の消費税額は、532円×10％＝53.2円→53円（小数点未満切捨）と求めます。
消費税額も税抜本体価格も存在しない税込金額とは
今回の記事では、先に結論から書いてしまいます。
消費税額を小数点未満切捨で求める場合、以下の条件に該当する税込商品価格については、消費税額も本体価格も数学的に「存在しない」ことになるのです。
記事タイトルの税込価格1,000円（税率10％）についても、11で割ると
1,000÷11＝90･･･10
となり、余りが10になるため、消費税額も税抜本体価格も数学的に「存在しない」ことになります。
(注)「･･･」は「余り」の意味です。小学生のときに使ってた表記です。
なぜこのようなことが起きるのか、以下、詳しく解説したいと思います。
税抜本体価格の求め方
まず、消費税額を小数点未満切捨で計算する前提で、税込金額から税抜本体価格を求める方法を解説します。
税込金額は既知の値としてわかっていいるため、税込金額をａとおきます。（ａは正の整数）
税抜本体価格は未知の値なのでｘとおきます。（ｘは正の整数）
消費税額は税抜本体価格に消費税率をかけて、小数点未満切捨てをした金額となります。
ここで、消費税率をｒとした場合、消費税額は「ガウス記号」を用いて、［ｒｘ］と表すことができます。
ガウス記号とは、以下のような性質を持つ関数で、床関数、フロアー関数、整数部分などと呼ばれることもあります。
ガウス記号
[ ]で表される関数。ある値を越えない最大の整数値を表す。X を実数，n を整数としたとき、n ≦ X ＜ n+1 ならば，[X]=n である。例えば，[2.34]=2，[-3.54]=-4。
税抜本体価格ｘと消費税額［ｒｘ］の合計額が税込金額ａとなるため、以下のような方程式を立てることができます。
ガウス記号を用いた関数の、以下の性質を用いて、ｒｘの範囲を求めます。
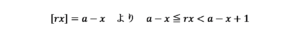上記の不等式からｘの範囲を求めると、次のようになります。
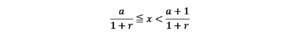
上記不等式の左辺に注目すると、ｘは、ａ÷（１＋ｒ）以上の整数値になることから、税抜本体価格ｘは、税込金額を（１＋消費税率）で割った金額を小数点未満切り上げした値になると結論付けることができます。
この計算方法を用いた消費税額の具体的な求め方については、詳しくは次の記事をご覧ください。
税抜金額ｘが整数の値を取らない場合の条件（標準税率10％の場合）
先ほど求めた不等式では、ｘが整数の値を取らず、税抜本体価格を求められないことがあります。
ここで、記事タイトルの「税込1,000円」の商品価格を例に考えてみましょう。
税込金額ａ＝1,000、消費税率ｒ＝0.1を代入すると
となるため、ｘは整数の値をとらないことになります。
これは、税抜本体価格は整数の値として存在しないということになり、税抜本体価格から求められる消費税額も同様に整数の値として存在しないということを意味します。
仮に、税込1,000円の税抜本体価格を909円とした場合、消費税額は909円×10％＝90.9円→90円（小数点未満切捨）、税込金額＝909円＋90円＝999円となり矛盾します。
一方、税込1,000円の税抜本体価格を910円とした場合、消費税額は910円×10％＝91円、税込金額＝910円＋91円＝1,001円となり、これまた矛盾します。
このように、税抜本体価格と消費税額が整数値として存在しないこととなる場合の条件について詳しく見ていきましょう。
まず、税抜本体価格・消費税額の求め方を整数論の問題として考えるため、剰余類による場合分けを考えます。
税込価格を（１＋消費税率）で割った式は、次のような整数同士の割り算の形で表すことができます。
したがって、税込価格をＡと表記し直した場合、以下の数式で表される11を法とする剰余類として考えることができます。（ｎ：ｎ≧０となる整数、ｍ：０≦ｍ≦10となる整数）
Ａ＝11ｎ＋ｍ
これを上記で求めたｘの不等式に当てはめて考えると、ｍ≠０（ｍ＝０の場合割り切れて整数値となるため）、かつ、以下のとおりAを（１＋ｒ）で割った整数部分と（A＋１）を（１＋ｒ）で割った数値の差が１以下となる場合には、ｘが整数値をとらないことになります。
すなわち、以下の条件式で表せます。
これにｒ＝0.1を代入して整理すると、次のように表せます。
上記不等式の左辺は、税込価格Ａを1.1で割った場合の小数部分を意味します。
したがって、Ａ＝11ｎ＋ｍと、11を法とする剰余類で分類しているため、剰余ｍに１から10までの各値を代入して1.1で割った10パターンの小数部分を見て、0.090909…以下となっているものがあれば、それが整数値の税抜本体価格を持たない剰余類となります。
エクセルの力を借りて、それぞれ計算すると以下のようになります。
ｍ＝10の場合、小数部分が0.090909…以下となるため、税抜本体価格ｘは整数値を取らないことになります。
つまり、標準税率10%が適用される場合、税込金額を11で割って余りが10になるときは、税抜本体価格及び消費税額は整数値として存在しないということになります。
税抜金額ｘが整数の値を取らない場合の条件（軽減税率８％の場合）
今度は、軽減税率8%が適用される場合について考えてみましょう。
考え方は先ほどと同じで、剰余類による場合分けを行います。
税込価格を（１＋消費税率）で割った式は、素因数分解をして次のような整数同士の割り算の形で表すことができます。
したがって、税込価格をＡと表記し直した場合、以下の数式で表される27を法とする剰余類として考えることができます。（ｎ：ｎ≧０となる整数、ｍ：０≦ｍ≦26となる整数）
Ａ＝27ｎ＋ｍ
これを上記で求めたｘの不等式に当てはめて考えると、ｍ≠０（ｍ＝０の場合割り切れて整数値となるため）、かつ、以下のとおりAを（１＋ｒ）で割った整数部分と（A＋１）を（１＋ｒ）で割った数値の差が１以下となる場合には、ｘが整数値をとらないことになります。
すなわち、以下の条件式で表せます。
これにｒ＝0.08を代入して整理すると、次のように表せます。
上記不等式の左辺は、税込価格Ａを1.08で割った場合の小数部分を意味します。
したがって、先ほどと同様、Ａ＝27ｎ＋ｍと、27を法とする剰余類で分類しているため、剰余ｍに１から26までの各値を代入して1.08で割った26パターンの小数部分を見て、0.074074…以下となっているものがあれば、それが整数値の税抜本体価格を持たない剰余類となります。
またまたエクセルの力を借りて、それぞれ計算すると以下のようになります。
ｍ＝13または26の場合、小数部分が0.074074…以下となるため、税抜金額ｘは整数値を取らないことになります。
つまり、軽減税率８%が適用される場合、税込金額を27で割って余りが13または26となるときは、税抜本体価格及び消費税額は整数値として存在しないということになります。
実際に、具体例としてｎ＝2021（今年の西暦）、ｍ＝13として税込金額Ａ＝2021×27＋13＝54,580円の場合の税抜本体価格について考えてみましょう。
税込金額ａ＝54,580、消費税率ｒ＝0.08を代入すると
となるため、ｘは整数の値をとらないことになり、すなわち、税抜本体価格及び消費税額は整数値として存在しないということになります。
（参考）適格請求書に記載する場合
令和5年10月1日からスタートする適格請求書等保存方式（インボイス制度）のもとでは、適格請求書等に消費税額を記載する必要があります。
適格請求書等保存方式のもとにおける積上計算の基礎となる消費税額等については、税込価格に110分の10（または108分の８）を乗じるか、税抜価格に100分の10（または100分の８）を乗じて、１円未満の端数が生じた時は、端数を切捨て、切上げ又は四捨五入により処理します。
（適格請求書に記載すべき消費税額等の計算）
第七十条の十 法第五十七条の四第一項第五号に規定する政令で定める方法は、次の各号に掲げる方法のいずれかとする。この場合において、当該各号に掲げる方法により算出した金額に一円未満の端数が生じたときは、当該端数を処理するものとする。
一 法第五十七条の四第一項第四号に規定する課税資産の譲渡等に係る税抜価額を税率の異なるごとに区分して合計した金額に百分の十（当該合計した金額が軽減対象課税資産の譲渡等に係るものである場合には、百分の八）を乗じて算出する方法
二 法第五十七条の四第一項第四号に規定する課税資産の譲渡等に係る税込価額を税率の異なるごとに区分して合計した金額に百十分の十（当該合計した金額が軽減対象課税資産の譲渡等に係るものである場合には、百八分の八）を乗じて算出する方法
（適格請求書に記載する消費税額等の端数処理）
問57 適格請求書には、税率ごとに区分した消費税額等の記載が必要であるとのことですが、消費税額等を計算する際の１円未満の端数処理はどのように行えばよいですか。【令和６年４月改訂】
【答】
適格請求書の記載事項である消費税額等に１円未満の端数が生じる場合は、一の適格請求書につき、税率ごとに１回の端数処理を行う必要があります（消令70の10、基通１－８－15）。 なお、切上げ、切捨て、四捨五入などの端数処理の方法については、任意の方法とすることができます。
適格請求書に記載する消費税額については、商品やサービスの価格を税込価格で表示しているか税抜価格で表示しているかにより異なります。
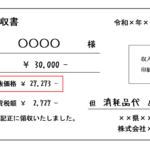
税込価格で表示している場合
商品やサービスの価格を税込価格で表示している場合の10％税込1,000円の消費税額は次のように計算します。
消費税額＝税込1,000円×10/110＝90.9090…円 →90円（切捨）or 91円（切上又は四捨五入）
よって、端数処理について「切捨て」を採用する場合は、下記のように表記します。
（税込価格：1,000円 消費税額：90円）
一方、端数処理について「切上げ」又は「四捨五入」を採用する場合は、下記のように表記します。
（税込価格：1,000円 消費税額：91円）
税抜価格で表示している場合
商品やサービスの価格を税抜価格で表示している場合の10％税込1,000円の消費税額の記載には注意が必要です。
適格請求書等に税抜価格を記載する場合は、「税抜価格×10/100」が消費税額となるように記載しなければなりません。
10％税込1,000円の税抜価格を整数値として記載する場合、1,000円×100/110＝909.0909…円となるため、近傍の「909円」か「910円」が候補となります。
ここで、それぞれについて「税抜価格×10/100」が消費税額となるように計算します。
［税抜価格を909円とする場合］
税抜価格を909円として採用する場合、消費税額は
909円×10/100＝90.9円
となるため、消費税額の端数処理について「四捨五入」又は「切上げ」を採用すれば、
消費税額は90.9円→91円とすることができ、税抜価格909円＋消費税額91円＝1,000円となり、ぴったり税込価格と一致させることができます。
［税抜価格を910円とする場合］
次に、税抜価格を910円として採用する場合について考えます。
この場合、消費税額は
910円×10/100＝91円
となります。
しかし、この場合、税抜価格910円＋消費税額91円＝1,001円となってしまい、税込価格が1,000円になりません。
つまり、適格請求書に税抜価格を表示することとしている場合、税抜価格を910円とすると矛盾が生じることになってしまうため、税抜価格を910円とすることはできず、税抜価格は909円とし、消費税額については「切上げ」又は「四捨五入」による端数処理を採用して91円と記載するしかありません。
まとめ
10％税込1,000円の商品やサービスの適格請求書等の記載方法は、代金を税込価格で表示しているか税抜価格で表示しているかにより異なります。
まとめ
消費税額を小数点未満切捨で求める場合、以下の条件に該当する税込商品価格については、消費税額も税抜本体価格も、整数値は数学的に「存在しない」こととなります。
