領収書を発行するときは、取引額の税込金額だけでなく、税抜金額も書くことが多いと思います。
しかし、税込価格から税抜価格を計算するのって、意外と大変じゃないですか？
例えば、以下のイラストのように、税込金額がキリのいい綺麗な数字のときは、たいてい税抜金額は汚い数字になります。
税抜金額や消費税額を求める際、「あれ、端数は切捨て？切り上げ？」と迷ってしまい、税抜金額と消費税額がそれぞれ本当に合っているか実際に検算したりなどで手間がかかり、意外と時間を食ってしまうことが多々あります。
そこで、今回は、請求書や領収書に記載する税抜価格と消費税額を確実かつ迅速に計算する方法について解説したいと思います。
請求書や領収書に税抜きの本体価格を記載する理由
そもそも、なぜ請求書や領収書に税抜金額も記載するのでしょうか？
実は、請求書や領収書に税込金額だけでなく税抜本体価格も記載すると、次のようなメリットがあるのです。
印紙税の節約になる
不動産売買契約書や不動産売渡証書、金銭借用証書、工事請負契約書、領収書などのことを「課税文書」といい、これらの文書を発行すると印紙税の納税義務が生じます。
印紙税は、税務署に直接税金を納めるのではなく、収入印紙を購入して契約書などに貼り付け、さらにその収入印紙に消印をする形で納税します。
印紙税の金額は、消費税額が明らかにわかる記載方法がされている場合は、消費税税抜きの本体価格（税抜価格）のみで判定を行います。（５万円未満の金額なら非課税となるため、収入印紙の貼付は不要となります。）
税抜価格が記載されていない場合は、税込価格で印紙税の金額を判定することになります。
したがって、領収書を発行する際は、税抜価格も記載した方が印紙税の節約になります。
源泉徴収額を少なくできる
源泉徴収税額は、報酬金額に10.21％（100万円を超える部分は20.42％）を乗じて算出しますが、源泉徴収の対象とすべき金額が税込金額なのか税抜金額なのかについて、国税庁のタックスアンサーには次のように記載されています。
弁護士や税理士などに報酬を支払った場合には、所得税及び復興特別所得税を源泉徴収することになっています。
この場合、源泉徴収の対象となる金額は、原則として、報酬・料金として支払った金額の全部、すなわち、消費税及び地方消費税(以下「消費税等」といいます。)込みの金額が対象となります。
ただし、弁護士や税理士などからの請求書等に報酬・料金等の金額と消費税等の額とが明確に区分されている場合には、消費税等の額を除いた報酬・料金等の金額のみを源泉徴収の対象としても差し支えありません。
つまり、源泉徴収の対象とすべき金額は、消費税の区分があれば、税込価格でも税抜価格でもどちらでもいいのです。
請求書や領収書に税込金額しか書いていない場合は、税込金額に10.21％（100万円を超える部分は20.42％）を乗じた金額を源泉徴収しなければなりません。
一方、請求書や領収書に税抜金額も記載されてる場合は、税抜金額に10.21％（100万円を超える部分は20.42％）を乗じた金額を源泉徴収することもできるため、源泉徴収額を少なくすることができます。
なお、この点については、詳しくは次の記事で解説しています。
消費税額の計算は小数点未満「切捨」を前提とする
商品価格の内訳として表示する消費税額の計算方法には、以下の３種類の方法があります。
商品価格の内訳として表示する消費税額は、その金額がそのまま税務署への納付税額になるわけではなく、あくまでも消費者に対して商品価格のうち消費税額がいくらぐらいなのかを示すためのものです。
したがって、どの方法で計算するかは法律等で特に決まっておらず、商品を販売する事業者の選択に委ねられています。
実際のところ、圧倒的大多数の事業者が①小数点未満切捨の方法により消費税の表示額を計算しているため、この記事では消費税額の計算はすべて税抜本体価格に消費税率を乗じて小数点未満切捨して求めるという前提で話を進めていきます。
例えば、税抜本体価格532円の商品（税率10％）の消費税額は、532円×10％＝53.2円→53円（小数点未満切捨）と求めます。
税抜金額の計算方法
請求書や領収書に記載する税抜金額はどうやって求めればいいのでしょうか？
先に結論から書くと、以下の方法で計算すれば、すぐに税抜金額を計算することができます。
消費税額は、上記で求めた税抜金額に消費税率をかけて、小数点未満を切り捨てて求めます。（または税込金額から上記で求めた税抜金額を差し引いて求めることもできます。）
税抜金額と消費税額を求める際は、必ず税抜金額から先に求めることに注意しましょう。
具体的な数値例
上記の方法をもとに、請求書や領収書に記載する税抜金額を実際に求めてみましょう。
税抜金額 ＝ 30,000円 ÷ 1.1 ＝ 27,272.7272…円 → 27,273円（小数点未満切上）
消費税額 ＝ 27,273円 × 10％ ＝ 2,727.3円 → 2,727円（小数点未満切捨）
（または、30,000円 － 27,273円 ＝ 2,727円）
合計：27,273円 ＋ 2,727円 ＝ 30,000円
となります。この場合の領収書は、すでに冒頭で出していますが以下のようになります。
税抜金額 ＝ 30,000円 ÷ 1.08 ＝ 27,777.7777…円 → 27,778円（小数点未満切上）
消費税額 ＝ 27,778円 × ８％ ＝ 2,222.24円 → 2,222円（小数点未満切捨）
（または、30,000円 － 27,778円 ＝ 2,222円）
合計：27,778円 ＋ 2,222円 ＝ 30,000円
となります。この場合の領収書は以下のようになります。
（注意）税抜本体価格及び消費税額が「存在しない」場合
消費税額を小数点未満切捨で求める場合、以下の条件に該当する税込商品価格については、消費税額も本体価格も数学的に「存在しない」ことになります。
なぜこのようなことが起きるのか、このような場合の商品価格の内訳表示はどうすればいいのかについては、詳しくは次の記事をご覧ください。
なぜ税込金額÷（１＋消費税率）の小数点未満の端数を切り上げるのか
なぜ上記の方法で税抜金額と消費税額を求めることができるのか、数学的に解説します。
まず、税込金額は既知の値としてわかっていいるため、税込金額をａとおきます。（ａは正の整数）
税抜金額は未知の値なのでｘとおきます。（ｘは正の整数）
消費税額は税抜金額に消費税率をかけて、小数点未満切捨てをした金額となります。
ここで、消費税率をｒとした場合、消費税額は「ガウス記号」を用いて、［ｒｘ］と表すことができます。
ガウス記号とは、以下のような性質を持つ関数で、床関数、フロアー関数、整数部分などと呼ばれることもあります。
ガウス記号
[ ]で表される関数。ある値を越えない最大の整数値を表す。X を実数，n を整数としたとき、n ≦ X ＜ n+1 ならば，[X]=n である。例えば，[2.34]=2，[-3.54]=-4。
税抜価格ｘと消費税額［ｒｘ］の合計額が税込金額ａとなるため、以下のような方程式を立てることができます。
ガウス記号を用いた関数の、以下の性質を用いて、ｒｘの範囲を求めます。
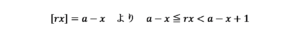上記の不等式からｘの範囲を求めると、次のようになります。
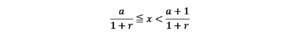
上記不等式の左辺に注目すると、ｘは、ａ÷（１＋ｒ）以上の整数値になることから、請求書や領収書に記載する税抜金額は、税込金額を（１＋消費税率）で割った金額を小数点未満切り上げした値になると結論付けることができます。
まとめ
請求書や領収書に記載する税抜価格及び消費税額は、次の方法で計算すれば確実かつ迅速に求めることができます。
消費税額：税抜価格 × 消費税率 → 小数点未満切捨
