前回の記事では、複数の事業を行っている場合の簡易課税制度による納付税額の計算方法について解説しました。
簡易課税による場合の適用されるみなし仕入率の計算方法には原則、特定1事業、特定2事業の3種類があります。
中でも、特定2事業の計算は有利になる組み合わせの判定までしないといけないため非常に計算に手間がかかりますが、実は特定２事業の特例計算で最も有利になる２事業の組み合わせを一瞬で見つける方法があることをご存知でしょうか？
今回は、簡易課税の特定２事業の最も有利な組み合わせを一瞬で見つける裏ワザについてご紹介したいと思います。
特定２事業の特例計算とは
特定２事業の特例計算は、全体の課税売上高のうち、特定の２事業の課税売上高の合計が占める割合が75％以上である場合に適用することができます。
この場合、その特定の２事業に係るみなし仕入率のうち低い方のみなし仕入率をその２事業以外の事業に適用して、原則に準じて計算した割合を適用されるみなし仕入率として控除対象仕入税額を計算します。
例えば、以下のような数値例の場合に、第１種事業と第３種事業の組み合わせで特定２事業の計算を行うときは、次のように計算します。
第１種事業と第３種事業のうち、みなし仕入率が低い方（第３種の70％）をその２事業（第１種と第３種）以外の事業に適用して、原則に準じて計算した割合（みなし仕入率で加重平均した割合）を適用されるみなし仕入率とします。
つまり、第１種にだけ90％のみなし仕入率をかけて、それ以外の事業には第３種事業の70％のみなし仕入率をかけて加重平均してみなし仕入率を求めます。
｛20,000円×90％＋（100,000円－20,000円）×70％｝÷100,000円＝74％
有利な組み合わせを一瞬で見つける裏技
特定２事業の特例計算では、特定の２事業の組み合わせのうちどの組み合わせが有利になるのか自分で見つけなければなりませんが、すべての組み合わせを検証するのは非常に手間がかかります。
ｎ種類の事業を行っている場合の２事業の組み合わせはnＣ2通りとなります（Cはコンビネーション）。
例えば、５種類の事業を行っている場合の２事業の組み合わせは5Ｃ2＝５×４÷(２×１)＝10通りもの数になります。
これらすべての組み合わせについて検証するのはとても大変です。
しかし、以下のような裏ワザを使えば、有利になる組み合わせを一瞬で見つけることができます。
いきなりこれだけ見たら「ちょっと何言ってるかわからないです」となるかと思うので、実際に数値例をもとに有利になる組み合わせを求めてみましょう。
数式や文章で説明しようとするとどうしても難しそうな表現になってしまいますが、感覚を掴めばすごく簡単です。
裏ワザの使い方
前回書いた記事↓で用いた数値と同じ金額を使って、特定２事業の特例計算を行う場合の最も有利となる組み合わせを裏ワザを使って求めてみましょう。
| 事業区分 | 業種別課税売上高（税抜） | 業種別消費税額（国税） |
| 第一種事業 | 500,000円 | 39,000円 |
| 第二種事業 | 1,300,000円 | 101,400円 |
| 第四種事業 | 400,000円 | 31,200円 |
| 第五種事業 | 7,600,000円 | 592,800円 |
| 第六種事業 | 200,000円 | 15,600円 |
| 合計 | 10,000,000円 | 780,000円 |
まず、上記の業種別課税売上高のうち最も大きいものは第５種事業の7,600,000円であるため、ｍ＝５となります。
次に、第５種事業よりもみなし仕入率が大きい事業は第１種、第２種及び第４種であるため、ｎ＝１，２，４となります。
この場合において、Ｔｎ×（ｍ－ｎ）が最も大きくなるｎを探します。
ｎ＝１の場合
ｎ＝１の場合、Ｔｎ（第１種事業の業種別消費税額）は39,000円となるため、Ｔｎ×(ｍ－ｎ)＝39,000円×(５－１)＝156,000円となります。
ｎ＝２の場合
ｎ＝２の場合、Ｔｎ（第２種事業の業種別消費税額）は101,400円となるため、Ｔｎ×(ｍ－ｎ)＝101,400円×(５－２)＝304,200円となります。
ｎ＝４の場合
ｎ＝４の場合、Ｔｎ（第４種事業の業種別消費税額）は31,200円となるため、Ｔｎ×(ｍ－ｎ)＝31,200円×(５－４)＝31,200円となります。
有利な組み合わせの判定
上記でそれぞれ求めたＴｎ×（ｍ－ｎ）のうち、最も大きくなるのはｎ＝２の場合であるため、特定２事業の特例計算で最も有利な組み合わせは第２種と第５種になります。
この組み合わせの求め方は、その業種の消費税額に、売上げが最も大きい業種の事業区分とその業種の事業区分の番号の差をかけるだけであり、暗算でもおおまかな金額でどれが一番大きくなるか求めることができるので、慣れれば有利な組み合わせを一瞬で判定することができます。
なお、上記で求めた金額はあくまでもどの組み合わせが有利になるのかの比較判定のためだけに用いるものであり、税額計算をする上では使わない数値なので注意しましょう。
上記の方法で有利な組み合わせを求めることができる理由
みなし仕入率は、（10ー事業区分の数値）×10％で求めることができます。
例えば、製造業などの第３種事業のみなし仕入率は(10 －３)×10％＝70％と求めることができます。
したがって、第ｎ種事業のみなし仕入率は（10ーｎ）×10％、第ｍ種事業のみなし仕入率は（10ーｍ）×10％と表すことができます。
したがって、特定２事業の特例計算を行う場合に適用されるみなし仕入率の分子の金額は、次のような数式で表すことができます。
ここで、第１項の算式のかっこの中に（ーｍ＋ｍ）を挿入してみると次のようになります。
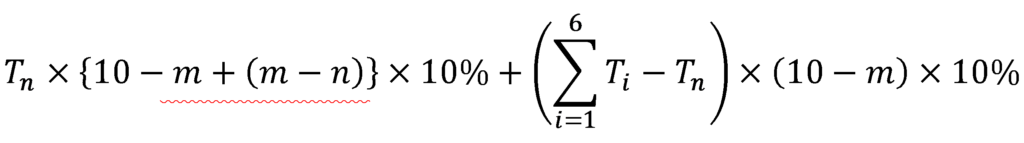
第１項のかっこの中を（10ーｍ）と（ｍ－ｎ）に分けて展開すると、次のようにちょうどＴｎ×(10ーｍ)×10％が前と後ろで相殺される形になります。
したがって、特定２事業の特例計算を行う場合に適用されるみなし仕入率の分子の金額は、次のように表すことができます。
上記算式中の未知の変数であるｎが含まれているのは前項のＴｎ×(ｍ－ｎ)×10％の部分だけです。
「×10％」はあってもなくても大小の比較に影響はないため、暗算でも計算しやすくするために「×10％」の部分は削ぎ落として、Ｔｎ×(ｍ－ｎ)が最も大きなるｎとｍの組み合わせが、特定２事業の特例計算において最も有利な組み合わせであると判定することができます。
数式の意味をもう少し分かりやすくするために、グラフを使って説明します。
例えば、第５種事業の売上げが最も大きい場合に第２種事業と第５種事業の組み合わせで特定２事業の特例計算を行う場合のみなし仕入率の分子は、第２種事業の消費税額×80％＋それ以外の事業の消費税額×50％となります。
この場合、第５種事業が最も売上げが大きいためｍ＝５、第２種事業が判定しようとしている事業なのでｎ＝２となります。
次の図の緑色の部分とピンク色の部分を合わせた金額が、特定２事業の特例計算を行う場合のみなし仕入率の分子の金額となります。
今回ご紹介した方法では、上記の図の見方を変えて、次の図の緑色の部分にのみ着目して最も有利な組み合わせを探していることになります。
まとめ
今回ご紹介した方法は、判定しようとしている業種の消費税額に、売上げが最も大きい業種の事業区分とその業種の事業区分の番号の差をかけて一番大きくなるものを探すだけなので、慣れれば暗算で有利な組み合わせを探すことができます。
これは僕自身が税理士受験生だったときに自分で考えた方法で、計算問題を解くときはいつもこの方法で有利な組み合わせを探していました。
この方法を使えば一瞬で最も有利な組み合わせを見つけることができ、計算スピードを大幅に上げることができるので、みなさんもぜひ使ってみてください。
