税理士試験の複数科目同時合格者数は何人？統計学的に推計してみた

税理士試験の受験生の方は、1回の試験で複数科目合格（２科目以上同時に合格）している人が何人くらいいるのだろうかと気になったことはありませんか？

国税庁のホームページでは、税理士試験の合格者数や合格率などの試験結果が公表されていますが、合格者数は実人員でしか発表されておらず、複数科目を同時に合格していたとしても１人としてカウントされるため、合格者の合格科目数を知ることはできません。

先日書いた記事の官報調整の有無の検証↓に必要なデータを入手するために、税理士試験の受験者の合格科目数に関する情報について国税庁に行政文書開示請求手続きを行ったのですが、合格者の合格科目数をまとめたデータはないとのことでした。

税理士試験の官報調整は本当にあるのか？統計学的に検証してみた

2020.5.17

税理士試験の受験生の間で、「官報リーチの受験生には官報調整が行われている」という都市伝説のような噂がまことしやかに語られています。 僕自身も受験生だったころ実際にこの噂を耳にしたことがあり、最後の１科目は大変ビビりながら受験したことを記憶しています。 この噂については「そんなの存在しないよ！」という...

いったんは諦めたのですが、やっぱりどうしても気になって仕方がありません。

一度気になりだしたら納得いくまで徹底的に調べないと気が済まない性格なので、何とかして合格者の合格科目数を知ることはできないかと色々と試行錯誤して考えたところ、統計学的に大まかな人数を推計する方法を思いついたのでご紹介します。

今回は「母比率の推定」という統計学の手法を用いて、令和元年度（第69回）税理士試験の合格者のうち複数科目に合格した人の人数を推計したいと思います。

合格者の延人員と実人員の差に着目

まず、複数科目に合格した人数を推計するために、国税庁のホームページで公表されている試験結果のうち、科目ごとの合格者の延べ人員と合格者数の実人員の差に着目します。

ここで、いったん簡単な具体例をもとに考えてみましょう。

例えば、科目１～３までの３種類の科目がある試験を、Ａ〜Ｆさんの６人が受験し、結果は以下の表のようになったとします。（「○」は合格、「×」は不合格、「－」は受けていない。）

科目１の合格者数は３人、科目２の合格者数は２人、科目３の合格者数は２人なので、合格者数の合計（延人員）は７人となります。

しかし、実人員の合格者は複数科目合格している人も１人としてカウントするため、合格者（実人員）はＡさん、Ｂさん、Ｄさん、Ｅさんの４人となります。

この場合、延べ人員の合格者数と実人員の合格者数の差は、複数科目合格者が１科目より多く合格した科目数の合計となります。

上記表の場合、延人員の合格者 （7人）と実人員の合格者（４人）との差（３人）は、複数科目合格者であるＢさんとＥさんが１科目より多く合格した科目数の合計を意味します（表中の青色の部分の数）。

延人員の合格者と実人員の合格者との差は、２科目合格者１人につき１、３科目合格者１人につき２、４科目合格者１人につき３、５科目合格者１人につき４増えることになります。

つまり、ｎ科目合格者の人数をＸｎとした場合、延人員の合格者と実人員の合格者との差（＝Ｄとする）は以下の数式で表すことができます。

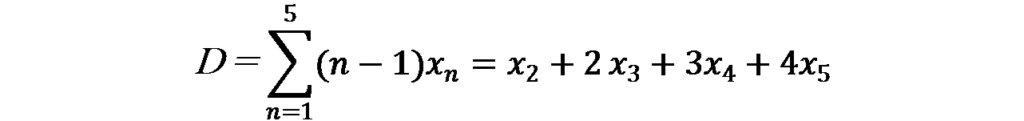
この関係を用いて、税理士試験の合格科目数ごとの合格者数の人数を推計したいと思います。

複数科目合格者の合格科目数の割合の推定

その前に、複数科目合格者の合格科目数ごとの割合を推計する必要があります。

国税庁からは合格科目数ごとの合格者の内訳は公表されていないため、「母比率の推定」という統計的手法を用いて、おおまかな割合を推定します。

今回は、複数科目合格者のうち、２科目合格者、３科目合格者、４科目合格者、５科目合格者の割合がそれぞれ何％であるかを推定するためのサンプルとして、資格学校ＴＡＣと資格の大原のホームページで公開されている合格報告（ＴＡＣ→令和元年度(69回)税理士試験　合格者喜びの声、大原→税理士講座喜びの声）のページで受講生の方から報告されている合格科目数を参考にして、２科目以上同時に合格している人が何人ずついるか集計しました。

集計結果（ＴＡＣ）↓

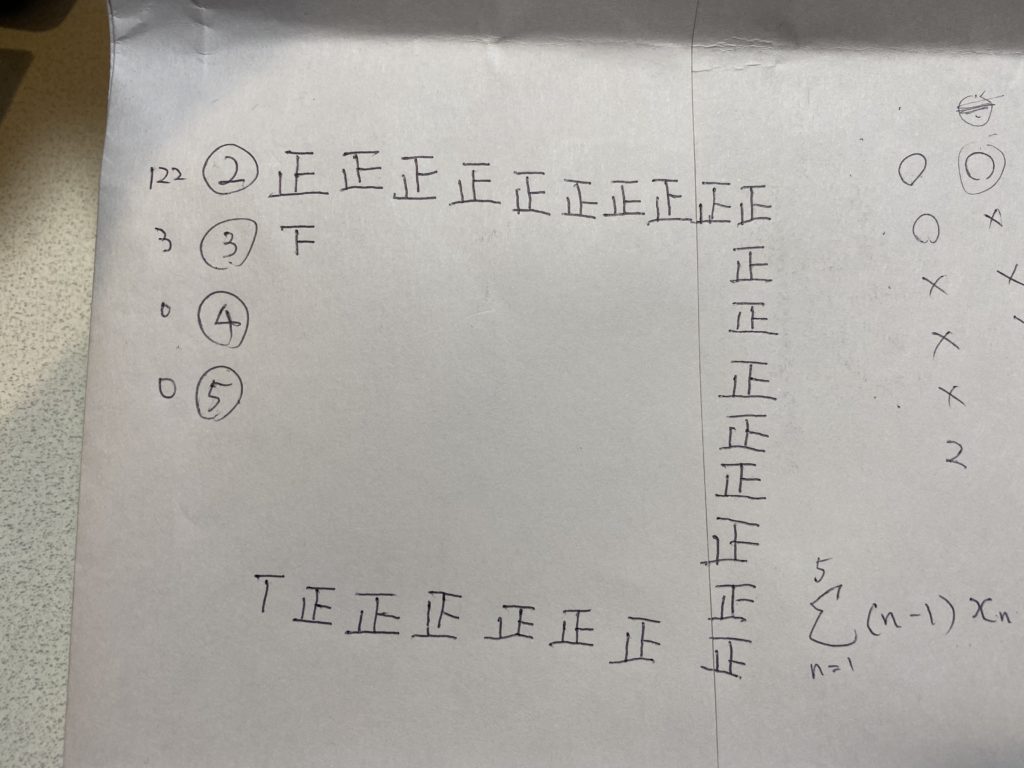
集計結果（大原）↓

集計の結果、複数科目合格者の人数は以下のようになりました。

これを見ると、3科目以上同時に合格するのがいかに難しいかがよく分かります。

４科目、５科目の同時合格者のサンプルは今回は検出されませんでした。実際に、４科目同時合格は実体験としてもほとんど聞いたことがないくらいごく稀であり、５科目同時合格に関しては数十年に一度いるかいないかの伝説レベルなのでほぼ０％に近いため、今回の検定では０％として取扱います。

上記の集計によると、サンプルとして抽出した複数科目合格者全体のうち３科目合格者が占める割合は11人÷241人＝4.5643･･･％となりました。

この標本比率をもとに、「母比率の推定」という統計的手法を用いて令和元年度（第69回）税理士試験の複数科目合格者全体のうち３科目合格者が占める割合ｐ（母比率）の推計を行います。

推定方法は、３科目合格者の占める割合pは、複数科目合格者数がnの場合は二項分布(ベルヌーイ分布)Ｂ(n,p)に従いますが、nが十分に大きいため、ド・モアブル＝ラプラスの極限定理により近似的に標本比率X/nが平均p、分散p(1-p)の正規分布Ｎ(p,p(1-p))に従うものとして95％信頼区間を求めます。

正規分布とは、以下の確率密度関数で表される山のような形をした確率分布で、統計学の世界でもっともよく使われている分布のひとつです。

（出典：AVILEN AI Trend）

この場合、母比率ｐの95%信頼区間は次の式で求められます。

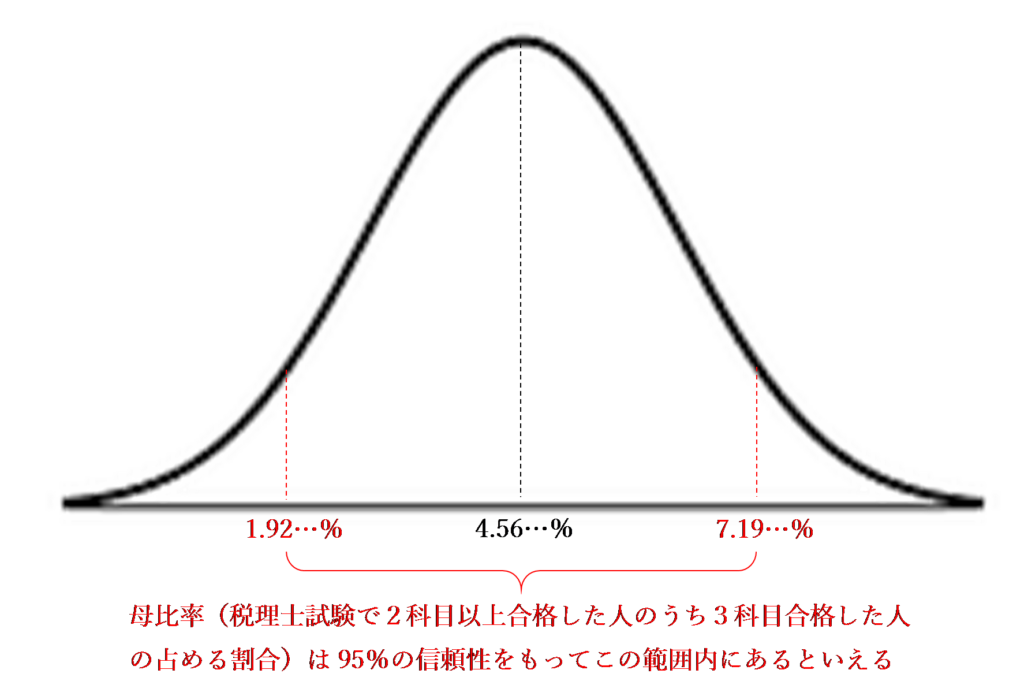
標本比率p^＝4.56％、サンプルサイズｎ＝241人を代入して整理すると次のようになります。

これは、複数科目合格者のうち３科目合格者が占める割合は約1.92％～7.19％の範囲内にあるということを意味します。

令和元年度（第69回）税理士試験の合格者を分析

国税庁が公表している令和元年度（第69回）税理士試験結果のデータによると、令和元年度（第69回）税理士試験の実人員の合格者数（一部科目合格、官報合格の合計）は5,388人、科目別の延人員の合格者数の合計は6,395人でした。

したがって、延人員の合格者と実人員の合格者との差は6,395人－5,388人＝1,007人となります。

この数値を先ほど示した次の数式にあてはめて、合格科目数の割合で割り返して複数科目合格者の人数を求めたいと思います。

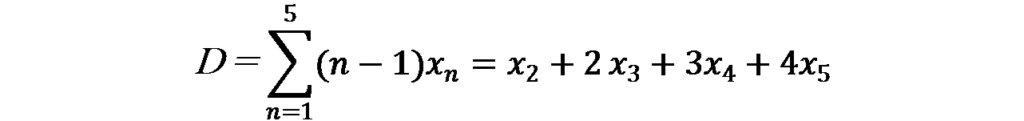
令和元年度（第69回）税理士試験で複数合格（２科目以上合格）した人数をＡ人、このうち３科目合格した人が占める割合をｐとすると、２科目合格者の人数はＸ２＝Ａ(1－p)、３科目合格者の人数はＸ３＝Ａｐと表せます。また、４科目・５科目合格した人は０人と仮定するするとＸ４＝０、Ｘ５＝０となり、以下のような方程式を立てることができます。

これをｐについて解くと次のようになります。

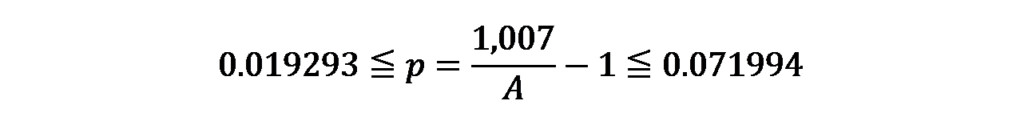
ｐが上記で求めた９５％信頼区間の範囲内にあるため、Ａの範囲は次のようになります。

つまり、令和元年度（第69回）税理士試験で複数合格（２科目以上合格）した人数は940人～987人であることがわかりました。

これにより、２科目合格者の人数Ａ(1－p)、３科目合格者の人数Ａｐについてもそれぞれ求めると

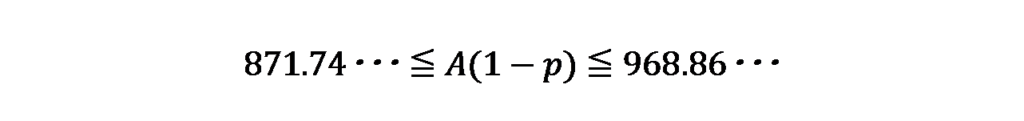
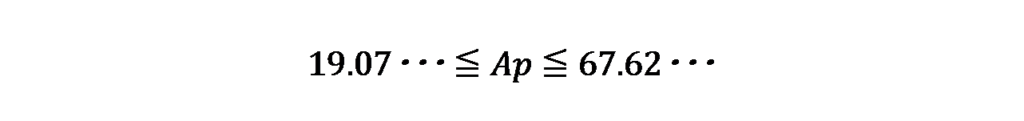
となります。

したがって、２科目合格者の人数は872人～968人、３科目合格者の人数は20人～67人の範囲内であることがわかりました。

また、合格者のうち１科目のみ合格した人数をＢとすると、Ｂの範囲は実人員の合格者の合計5,388人から複数科目合格者の範囲を差し引いて次のように求めることができます。

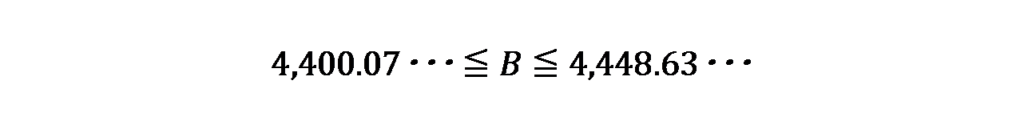
したがって、令和元年度（第69回）税理士試験で１科目のみ合格した人数は4,401人～4,448人であることがわかりました。

なお、０科目合格者（１科目も合格できなかった人）の人数は、実人員の全受験者数から合格者数を引いて29,779人－5,388人＝24,391人と求められます。

まとめ

以上の検証から、令和元年度（第69回）税理士試験の受験者の合格科目数のおおまかな内訳は、95％の信頼性をもって、以下の表のとおりになることがわかりました。（端数処理の関係上、合計はぴったり一致しません。）

なお、人数・割合の分布のパターンは同じ色同士で対応します。

例えば、１科目合格者が4,401人に近かった場合、２科目合格者は968人に近く、３科目合格者は20人に近くなり、それぞれの赤色の数字に近くなります。逆に、１科目合格者が4,448人に近かった場合、２科目合格者は872人に近く、３科目合格者は67人に近くなり、それぞれの青色の数字に近くなります。

４科目同時合格者はもしかしたら１人くらいはいるかもしれませんが、確率としては低いと思います。５科目同時合格者はいたら新聞とかに載るくらいの話題になると思いますが、今のところそういった情報はないためいないと思います。

（追記）単科目受験生を除いた統計結果

Twitterでこの記事の統計結果がプチバズりし、フォロワーの方から「単科目受験生を除いた統計結果（＝２科目以上受験した受験生の同時科目合格率）も知りたい」という意見がありました。

今回の分析で用いた令和元年分の本試験結果については、以前書いた官報調整の有無に関する検証の記事↓で、国税庁に行政文書開示請求手続きを行っており、受験生が何科目受験したのかのデータを独自に入手しています。

税理士試験の官報調整は本当にあるのか？統計学的に検証してみた

2020.5.17

税理士試験の受験生の間で、「官報リーチの受験生には官報調整が行われている」という都市伝説のような噂がまことしやかに語られています。 僕自身も受験生だったころ実際にこの噂を耳にしたことがあり、最後の１科目は大変ビビりながら受験したことを記憶しています。 この噂については「そんなの存在しないよ！」という...

上記表は、行政文書開示請求手続きで独自に入手したデータで、ピンク色のマスの受験者数の合計（91人＋102人＋1070人＋8569人＝9,832人）が２科目以上同時に受験した受験生の人数となります。

なお、３科目以上同時に受験した受験生の人数は（91人＋102人＋1070人＝1,263人）となります。

これをもとに、令和元年の本試験で複数科目同時に受験した受験生が、複数科目同時に合格する割合を計算すると次の表のようになります。

（感想）

全合格者5,388人のうち、１科目合格者（4,401人～4,448人）が占める割合は81.6％～82.5％であることを鑑みると、１回の試験で２科目以上同時に合格することがいかに難しいことかよくわかりました。

それと、統計学の力は本当にすごいと改めて思いました。見えなかったものがここまで可視化できるようになるとすごく気持ちが良いです。

やはり統計学は最強の学問です。

統計学が最強の学問である

created by Rinker

• Amazon
• 楽天市場
• Yahooショッピング

マンガでわかる統計学 素朴な疑問からゆる~く解説 (サイエンス・アイ新書)

created by Rinker

• Amazon
• 楽天市場
• Yahooショッピング