前回書いた記事では、役員や従業員に食事を支給した場合の消費税の取扱いについて解説しました。
今回は、役員や従業員に支給した食事代に標準税率10％と軽減税率８％が混在している場合に、福利厚生費として計上する課税仕入れの最も有利な金額を「線形計画法」という数学的な手法によって計算する方法をご紹介したいと思います。
線形計画法とは
まず、線形計画法とは何かについて説明します。
線形計画法とは、一次式で制約条件を記述し、その制約条件の中で目標値が最大又は最小となる値を求める数学的な手法をいいます。
一次の不等式または一次式で表される制約条件のもとで、一次式で表される目的関数を最大または最小にする値を求める数学的手法。生産計画・輸送計画などに応用される。リニアプログラミング。LP（linear programming）。
変数がたくさんある場合は大学レベルの線形代数の考え方が必要になりますが、変数が2つだけでｘｙ平面で考える場合については高校数学で習う話になります。
この記事で紹介する方法は、「標準税率10％課税仕入れの税抜金額」と「軽減税率８％課税仕入れの税抜金額」という２変数で考えるため、ｘｙ平面だけで考えます。
線形計画法の例題
例えば、以下のような４つの制約式があったとします。
これらの制約条件を満たす解の領域は、以下のグラフの青色で示した部分のようになります。
ここで、目的関数：Ｚ＝ｘ＋ｙの値を最大化する変数の値を求めます。
ｘ＋ｙは、
と
の２つのベクトルの内積となります。
ここで、ベクトルｐへのベクトルｑの正射影ベクトル（ベクトルｖとする）について考えてみましょう。
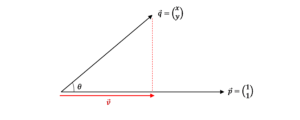
ベクトルｐとベクトルｑのなす角をθとして、内積について考えると以下のような関係式が得られます。
ベクトルｐの成分がともに正の場合、制約条件を満たす解の領域が第一象限、0≦x のx軸上または 0≦y のy軸上にあるときは０°≦θ＜90°となるため、内積はプラスの値となります。
よって、正射影ベクトルｖの大きさは、ベクトルｐとベクトルｑの内積に正比例することになるため、「一次式ｘ＋ｙを大きくしたい」⇔「(x,y) の (1,1) への正射影ベクトルの大きさを大きくしたい」⇔「できるだけ(1,1) の方向へ進みたい」と言い換えることができます。
したがって、制約条件の中で目的関数を最大化する最適解は、を法線ベクトルとする等高線をずらしていき、原点から最も遠い等高線が通る点（20,40）が最適解となり、最大値は20＋40＝60となります。
この考え方を、役員や従業員に食事を支給した場合における、消費税額の計算上最も有利な福利厚生費の計上額の計算に応用してみましょう。
役員や従業員に食事を支給した場合の制約条件
役員や従業員に食事を支給する場合、会社が負担した食事代の一部を「福利厚生費」として計上し、消費税法上も課税仕入れとして処理することができます。
課税仕入れの金額が大きくなるほど仕入税額控除できる金額が大きくなるため、課税仕入れの金額は大きいほど有利になります。
しかし、会社が役員や従業員に提供する食事代には、仕出し弁当や食材の購入費用などの軽減税率８％が適用される課税仕入れや、契約食堂における食事の提供など標準税率10％が適用される課税仕入れもあるため、福利厚生費として計上する課税仕入れの税率ごとの内訳をいくらずつにすべきかは意外と複雑でとっさに判断がつかないところであります。
そこで、国税庁のタックスアンサーNo.2594『食事を支給したとき』に記載されている要件を線形計画法における制約条件とみなして、福利厚生費として計上する課税仕入れの税込金額を最大化する方法を考えてみましょう。
役員や使用人に支給する食事は、次の二つの要件をどちらも満たしていれば、給与として課税されません。
(1) 役員や使用人が食事の価額の半分以上を負担していること。
(2) 次の金額が1か月当たり3,500円（税抜き）以下であること。
(食事の価額)－(役員や使用人が負担している金額)この要件を満たしていなければ、食事の価額から役員や使用人の負担している金額を差し引いた金額が給与として課税されます。
ここで、最大値を求めるにあたって、以下のように数式をおきます。
| 当事業年度中の標準税率10％が適用される食事代の総額（税抜き） | ａ円 |
| 当事業年度中の軽減税率８％が適用される食事代の総額（税抜き） | ｂ円 |
| 当事業年度中の福利厚生費として計上できる会社負担の食事代のうち10％課税仕入れとなる金額（税抜き） | ｘ円 |
| 当事業年度中の福利厚生費として計上できる会社負担の食事代のうち８％課税仕入れとなる金額（税抜き） | ｙ円 |
| 当事業年度の月数 | ｍか月 |
| 役員・従業員の数 | ｎ人 |
この場合、上記タックスアンサーの要件は、以下の制約式で表すことができます。
当事業年度の「福利厚生費」として計上する課税仕入れに係る税額（＝仕入税額控除される金額）は「0.1ｘ＋0.08ｙ」と表すことができるため、仕入税額控除できる金額の最大値を求めることは、上記①～④の制約条件において目的関数：Ｚ＝0.1ｘ＋0.08ｙを最大化する最適解を求める線形計画法の問題として考えることができます。（国税部分のみに着目して目的関数を「0.078ｘ＋0.0624ｙ」とおいた場合でも、標準税率と軽減税率の国税の比率は地方消費税を含む場合と同じなので計算結果は同じになります。）
この場合、ａとｂの金額に応じて、次の５パターンに場合分けをしてそれぞれ考えます。ａとｂの金額がいくらであっても、必ず以下の５つのパターンのいずれかに当てはまります。
① 7,700ｍｎ＜1.1ａ＋1.08ｂ，かつ，3,500ｍｎ＜ａ の場合
下記の２つの制約条件を満たす解の領域は、次のグラフの青色の部分のようになります。
会社が役員や従業員に食事を多く支給しており、外食など標準税率10％が適用される食事代が多い場合は下記のようになります。
ここで、目的関数：Ｚ＝0.1ｘ＋0.08ｙの値を最大化する変数の値を求めます。
0.1ｘ＋0.08ｙは、「標準税率10％」と「軽減税率８％」を成分とするベクトル
と、福利厚生費として計上する「10％課税仕入れの金額ｘ（税抜）」と「８％課税仕入れの金額ｙ（税抜）」を成分とするベクトルの２つのベクトルの内積となります。
したがって、制約条件の中で目的関数を最大化する最適解は、を法線ベクトルとする等高線をずらしていき、原点から最も遠い等高線が通る点（3,500mn，０）が最適解となります。
福利厚生費の計上額は1.1ｘ＋1.08ｙと表せるため、この場合の福利厚生費は1.1×3,500ｍｎ＋1.08×0＝3,850ｍｎとなります。
なお、福利厚生費として計上する会社負担の食事代のうち、最も有利な10％課税仕入れと８％課税仕入れの税込金額はそれぞれ次のようになります。
仕訳を数式で示すと以下のようになります。
（注）「立替金」は役員・従業員の負担額です。
例えば、当社の役員及び従業員数は10人（＝ｎ）（年を通じて変動はない）、当事業年度は４月１日から３月31日までの12か月（＝ｍ）であり、当事業年度中に役員及び従業員に提供した食事代のうち標準税率10％が適用される金額は550,000円（税抜500,000円（＝ａ））、軽減税率８％が適用される金額は432,000円（税抜400,000円（＝ｂ））である場合は、最も有利な10％課税仕入れと８％課税仕入れの税込金額はそれぞれ次のようになります。
標準税率10％課税仕入れ：3,850×12×10＝462,000円
軽減税率８％課税仕入れ：０円
この場合の仕訳は以下のようになります。
② 7,700ｍｎ＜1.1ａ＋1.08ｂ，かつ，ａ≦3,500ｍｎ の場合
下記の２つの制約条件を満たす解の領域は、次のグラフの青色の部分のようになります。
会社が役員や従業員に食事を多く支給しており、弁当や食材など軽減税率８％が適用される食事代が多い場合は下記のようになります。
制約条件の中で目的関数：Ｚ＝0.1ｘ＋0.08ｙを最大化する最適解は、を法線ベクトルとする等高線をずらしていき、原点から最も遠い等高線が通る点（ａ，3,500mn－ａ）が最適解となります。
福利厚生費の計上額は1.1ｘ＋1.08ｙと表せるため、この場合の福利厚生費は1.1×ａ＋1.08×（3,500ｍｎ－ａ）＝3,780ｍｎ＋0.02ａとなります。
なお、福利厚生費として計上する会社負担の食事代のうち、最も有利な10％課税仕入れと８％課税仕入れの税込金額はそれぞれ次のようになります。
仕訳を数式で示すと以下のようになります。
（注）「立替金」は役員・従業員の負担額です。
例えば、当社の役員及び従業員数は10人（＝ｎ）（年を通じて変動はない）、当事業年度は４月１日から３月31日までの12か月（＝ｍ）であり、当事業年度中に役員及び従業員に提供した食事代のうち標準税率10％が適用される金額は440,000円（税抜400,000円（＝ａ））、軽減税率８％が適用される金額は540,000円（税抜500,000円（＝ｂ））である場合は、最も有利な10％課税仕入れと８％課税仕入れの税込金額はそれぞれ次のようになります。
標準税率10％課税仕入れ：1.1×400,000＝440,000円
軽減税率８％課税仕入れ：3,780×12×10－1.08×400,000＝21,600円
この場合の仕訳は以下のようになります。
③ 1.1ａ＋1.08ｂ≦7,700ｍｎ，かつ，1.08ｂ＜1.1ａ の場合
下記の２つの制約条件を満たす解の領域は、次のグラフの青色の部分のようになります。
会社が役員や従業員にあまり多く食事を支給しておらず、外食などの標準税率10％が適用される食事代が多い場合は下記のようになります。
制約条件の中で目的関数：Ｚ＝0.1ｘ＋0.08ｙを最大化する最適解は、を法線ベクトルとする等高線をずらしていき、原点から最も遠い等高線が通る点（(1.1ａ＋1.08ｂ)/2.2，０）が最適解となります。
この場合の福利厚生費は1.1×（1.1ａ＋1.08ｂ）/2.2＋1.08×０＝0.55ａ＋0.54ｂとなります。
なお、福利厚生費として計上する会社負担の食事代のうち、最も有利な10％課税仕入れと８％課税仕入れの税込金額はそれぞれ次のようになります。
仕訳を数式で示すと以下のようになります。
（注）「立替金」は役員・従業員の負担額です。
例えば、当社の役員及び従業員数は10人（＝ｎ）（年を通じて変動はない）、当事業年度は４月１日から３月31日までの12か月（＝ｍ）であり、当事業年度中に役員及び従業員に提供した食事代のうち標準税率10％が適用される金額は550,000円（税抜500,000円（＝ａ））、軽減税率８％が適用される金額は216,000円（税抜200,000円（＝ｂ））である場合は、最も有利な10％課税仕入れと８％課税仕入れの税込金額はそれぞれ次のようになります。
標準税率10％課税仕入れ：0.55×500,000＋0.54×200,000＝383,000円
軽減税率８％課税仕入れ：０円
この場合の仕訳は以下のようになります。
④ 1.1ａ＋1.08ｂ≦7,700ｍｎ，かつ，1.1ａ≦1.08ｂ，かつ，1.06ａ＋1.08ｂ≦7,560ｍｎ の場合
下記の３つの制約条件を満たす解の領域は、次のグラフの青色の部分のようになります。
会社が役員や従業員にあまり多く食事を支給しておらず、弁当や食材などの軽減税率８％が適用される食事代が多い場合は下記のようになります。
（注）⑶の式中の「1.06ａ」を見て「なにこれ？税率６％！？」と思われるかもしれませんが、⑶の式は制約式の交点のｘ座標よりａが大きくなる場合の条件を計算するとこうなります。
制約条件の中で目的関数：Ｚ＝0.1ｘ＋0.08ｙを最大化する最適解は、を法線ベクトルとする等高線をずらしていき、原点から最も遠い等高線が通る点（ａ，ｂ/2－0.55ａ/1.08）が最適解となります。
この場合の福利厚生費は1.1×ａ＋1.08×（ｂ/2－0.55ａ/1.08）＝0.55ａ＋0.54ｂとなります。
なお、福利厚生費として計上する会社負担の食事代のうち、最も有利な10％課税仕入れと８％課税仕入れの税込金額はそれぞれ次のようになります。
仕訳を数式で示すと以下のようになります。
（注）「立替金」は役員・従業員の負担額です。
例えば、当社の役員及び従業員数は10人（＝ｎ）（年を通じて変動はない）、当事業年度は４月１日から３月31日までの12か月（＝ｍ）であり、当事業年度中に役員及び従業員に提供した食事代のうち標準税率10％が適用される金額は220,000円（税抜200,000円（＝ａ））、軽減税率８％が適用される金額は540,000円（税抜500,000円（＝ｂ））である場合は、最も有利な10％課税仕入れと８％課税仕入れの税込金額はそれぞれ次のようになります。
標準税率10％課税仕入れ：1.1×200,000＝220,000円
軽減税率８％課税仕入れ：0.54×500,000－0.55×200,000＝160,000円
この場合の仕訳は以下のようになります。
⑤ 1.1ａ＋1.08ｂ≦7,700ｍｎ，かつ，1.1ａ≦1.08ｂ，かつ，7,560ｍｎ＜1.06ａ＋1.08ｂの場合
下記の３つの制約条件を満たす解の領域は、次のグラフの青色の部分のようになります。
会社が役員や従業員に支給した食事代が１人あたりだいたい月7,000円付近で、そのうち弁当や食材などの軽減税率８％が適用される食事代が大半であり、外食などの標準税率10％が適用される食事代が僅少である場合は下記のようになります。（このパターンになるのはレアケースです。）
制約条件の中で目的関数：Ｚ＝0.1ｘ＋0.08ｙを最大化する最適解は、を法線ベクトルとする等高線をずらしていき、原点から最も遠い等高線が通る点（ａ，3,500mn－ａ）が最適解となります。
福利厚生費の計上額は1.1ｘ＋1.08ｙと表せるため、この場合の福利厚生費は1.1×ａ＋1.08×（3,500ｍｎ－ａ）＝3,780ｍｎ＋0.02ａとなります。
なお、福利厚生費として計上する会社負担の食事代のうち、最も有利な10％課税仕入れと８％課税仕入れの税込金額はそれぞれ次のようになります。
仕訳を数式で示すと以下のようになります。
（注）「立替金」は役員・従業員の負担額です。
例えば、当社の役員及び従業員数は10人（＝ｎ）（年を通じて変動はない）、当事業年度は４月１日から３月31日までの12か月（＝ｍ）であり、当事業年度中に役員及び従業員に提供した食事代のうち標準税率10％が適用される金額は39,600円（税抜36,000円（＝ａ））、軽減税率８％が適用される金額は869,400円（税抜805,000円（＝ｂ））である場合は、最も有利な10％課税仕入れと８％課税仕入れの税込金額はそれぞれ次のようになります。
標準税率10％課税仕入れ：1.1×36,000＝39,600円
軽減税率８％課税仕入れ：3,780×12×10－1.08×36,000＝414,720円
この場合の仕訳は以下のようになります。
計算にあたっての注意点
（注1）月ごとの福利厚生費を計算する場合は「ｍ=1」として考える
上記の計算方法は、当事業年度中の食事代に係る福利厚生費を決算時にまとめて計上する場合を想定してご紹介しています。
月ごとの食事代に係る福利厚生費を計算する場合は、ａ、ｂ、ｘ、ｙを「当事業年度中の金額」ではなく「今月中の金額」として考え、当事業年度の月数について「ｍ=1」として考えれば求められます。
（注2）円未満の端数は切り捨てる
計算過程で円未満の端数が生じた場合は、四捨五入や切り上げなどをすると国税庁のタックスアンサーの要件（会社負担額が半分以下、１月あたり税抜3,500円以下）を満たさなくなってしまうおそれがあるため、円未満の端数はすべて切り捨てをして計算してください。
（注3）通常の勤務時間外において支給する食事代は考慮しない
残業、宿直、日直等（休日労働も含む。）の通常の勤務時間外において会社が従業員・役員に対して支給する食事については、「会社の負担割合」や「会社の負担金額」に関係なく、食事代金の全額を「福利厚生費」として計上することができます。
そのため、上記の線形計画法による計算では、通常の勤務時間外において会社が従業員・役員に対して支給した食事の代金は除外して計算を行うことに注意しましょう。
まとめ
| 当事業年度中の標準税率10％が適用される食事代の総額（税抜き） | ａ円 |
| 当事業年度中の軽減税率８％が適用される食事代の総額（税抜き） | ｂ円 |
| 当事業年度中の福利厚生費として計上できる会社負担の食事代のうち10％課税仕入れとなる金額（税抜き） | ｘ円 |
| 当事業年度中の福利厚生費として計上できる会社負担の食事代のうち８％課税仕入れとなる金額（税抜き） | ｙ円 |
| 当事業年度の月数 | ｍか月 |
| 役員・従業員の数 | ｎ人 |
上記のように数式を置いた場合、
役員や従業員に食事を支給した場合に福利厚生費として計上できる会社負担額の最も有利な10％課税仕入れと８％課税仕入れの税込金額は、「線形計画法」で計算すると、次のようになります。どんな場合であっても、５つの条件のいずれかには必ず当てはまります。
| 条件（不等式をすべて満たすこと） | 標準税率10％課税仕入れの税込金額 | 軽減税率８％課税仕入れの税込金額 |
|
7,700ｍｎ＜1.1ａ＋1.08ｂ 3,500ｍｎ＜ａ |
3,850ｍｎ円 | ０円 |
|
7,700ｍｎ＜1.1ａ＋1.08ｂ ａ≦3,500ｍｎ |
1.1ａ円 | 3,780ｍｎ－1.08ａ円 |
|
1.1ａ＋1.08ｂ≦7,700ｍｎ 1.08ｂ＜1.1ａ |
0.55ａ＋0.54ｂ円 | ０円 |
|
1.1ａ＋1.08ｂ≦7,700ｍｎ 1.1ａ≦ 1.08ｂ 1.06ａ＋1.08ｂ≦7,560ｍｎ |
1.1ａ円 | 0.54ｂ－0.55ａ円 |
|
1.1ａ＋1.08ｂ≦7,700ｍｎ 1.1ａ≦ 1.08ｂ 7,560ｍｎ＜1.06ａ＋1.08ｂ |
1.1ａ円 | 3,780ｍｎ－1.08ａ円 |
（注）上記の計算式は当事業年度中の福利厚生費の総額です。月ごとの福利厚生費を計算する場合は、ａ、ｂ、ｘ、ｙの「当事業年度中の」を「今月中の」に読み替え、「ｍ=1」として考えれば求められます。
この計算方法は国税庁等が公表しているものではなく、僕がオリジナルで考えた方法です。なぜかバイクで走っているときにふと思いつきました。
公式として活用していただけたら幸いです。
