法律上の期間の計算方法は独特な言い回しが多く、具体的な日付がいつなのかわからなくなってしまうことがあるかと思います。
税法の世界では、申告書や届出書をいつまでに提出しなけばならないのかという期日や、納税義務等の判定の基準となる期間がいつからいつまでなのかを１日でも間違えてしまったら、課税関係が大きく変わってしまうため、期間の計算方法については明確に把握しておく必要があります。
期間という抽象的な概念をどのようにイメージするかは人それぞれかと思いますが、僕は期間を考える際はいつも１次元のタイムテーブルではなく、２次元の階段状のグラフを頭の中でイメージしながら計算していました。
そこで今回は、法律上の期間の計算方法について「フロアー関数」のグラフを使って考える方法について解説します。
なお、この考え方は既存の判例や学説の解説ではなく、僕が独自に考えた完全にオリジナルの発想なので予めご了承ください。
日付けと時刻の関係を階段状のグラフとして捉える
日時を１本の数直線で捉えるのではなく、日付と日時の２軸の二次元グラフで考えてみます。
例えば、「2020年４月１日」という日付が示す期間をXとすると、Xは以下の時刻の範囲内の期間として表すことができます。
2020年４月１日0:00 ≦ X ＜ 2020年４月２日0:00
この関係について、日付（〇月〇日）を整数部分、時刻（〇時〇分）を小数部分と見立てて考えた場合、以前書いた記事「中間納付額の消費税と地方消費税の内訳の計算方法②（数学的証明）」でも登場したフロアー関数（床関数）としてグラフを書くことができます。
この場合、日付と日時の関係性を示すグラフは以下のようになります。
上記グラフのうち、黒丸●については端点（午前０時）を含み、白丸○は端点（午前０時）を含みません。
これは、１日は０時０分０秒から23時59分59.9999…秒まで続き、24時０分０秒（＝０時０分０秒）になったら日付が変わることを意味しています。
１日の始まりは「０時０分０秒」という時刻で表すことができますが、１日の終わりについては「23時59分59.9999…秒」と小数点以下が無限に続くため、具体的な時刻で表すことができません。そのため、１日の終わりを指し示す時刻は存在しないということになります。
数学的な用語でいうと、「１日」は「半開区間（左閉右開区間）の集合」として捉えることができます。
これを踏まえて、法律上の期間の計算方法について考えてみたいと思います。
税法上の期間の計算方法は国税通則法に規定されている
税法の世界における期間の計算方法は国税通則法第10条第１項において、以下のように規定されています。なお、この規定は民法第139～143条と同様に取扱うことの確認規定として設けられたものであるため、民法上の期間計算の方法とほぼ同じです。
第十条 国税に関する法律において日、月又は年をもつて定める期間の計算は、次に定めるところによる。
一 期間の初日は、算入しない。ただし、その期間が午前零時から始まるとき、又は国税に関する法律に別段の定めがあるときは、この限りでない。
二 期間を定めるのに月又は年をもつてしたときは、暦に従う。
三 前号の場合において、月又は年の始めから期間を起算しないときは、その期間は、最後の月又は年においてその起算日に応当する日の前日に満了する。ただし、最後の月にその応当する日がないときは、その月の末日に満了する。
上記の太字で示した第１項の規定について、次のように言い換えることができます。
これは一体どういうことなのか。実際にグラフを使って考えてみましょう。
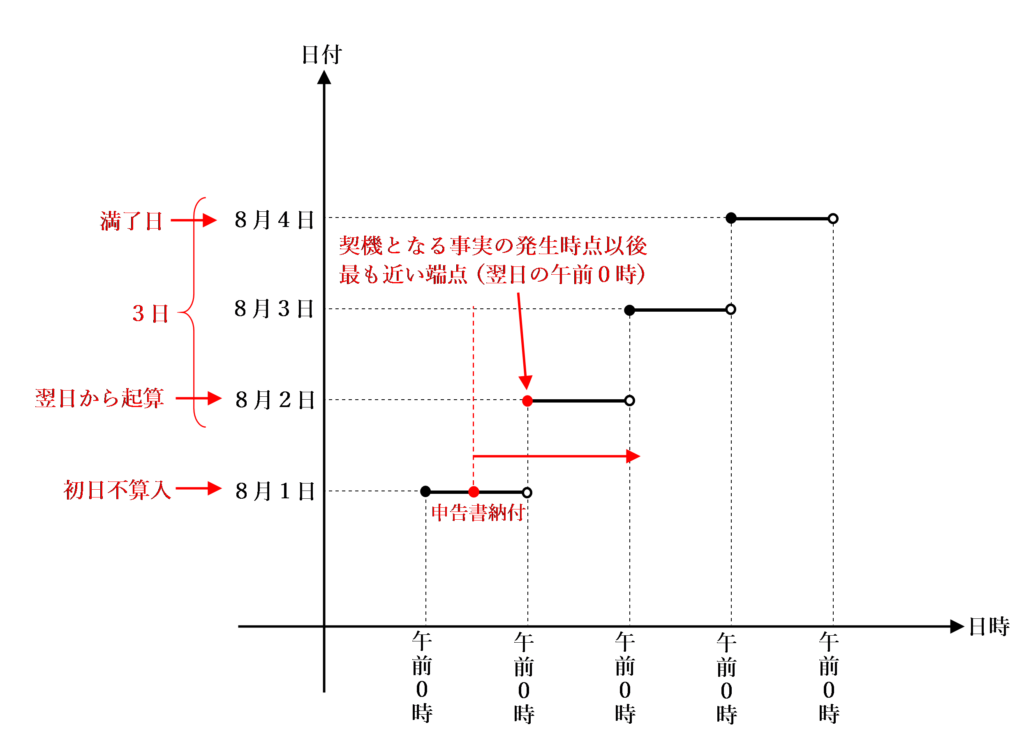
初日不算入となる場合
原則として、期間の初日は算入せずに、翌日を起算日とします。
初日不算入となる場合の具体例としては、以下のようなものがあります。
・納付の日から３日以内
・○○を知った時から５年以内 など
これらの共通点は「期間計算開始の契機となる事実が１日の途中で生じている」ということです。
厳密に期間を計算するなら、その事実が生じた時点から期間計算を開始すべきですが、現実的にはその事実が生じた時刻を正確に証明することは困難です。
したがって、その事実が生じた時点以後の最も近い端点（翌日の午前０時）から期間計算を開始します。
例えば、国税徴収法第131条（配当計算書）の「納付の日から３日以内」というのは、８月１日に申告書を納付した場合は、納付の日の翌日から起算して３日を満了する８月４日までということになります。
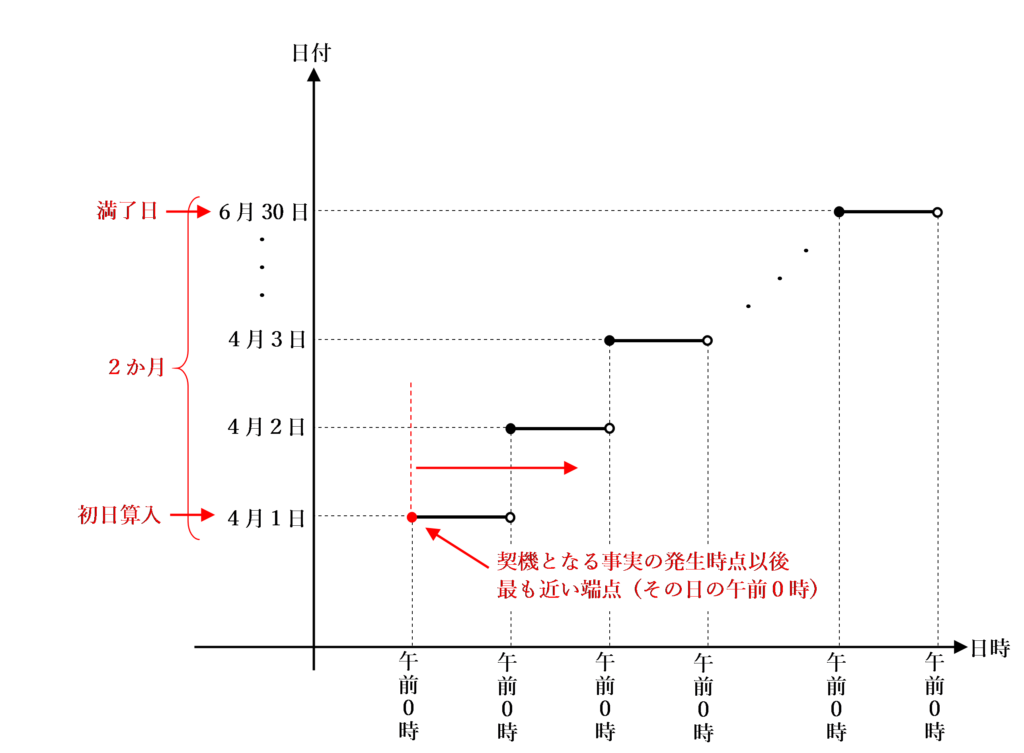
初日算入となる場合
原則は期間の初日は不算入ですが、その期間が午前０時から始まるときは初日を起算日（初日算入）として計算します。
初日算入となる場合の具体例としては、以下のようなものがあります。
・相続があった日の翌日からその年の12月31日まで
・令和２年４月１日から など
これらの共通点は「期間計算開始の契機となる事実が１日の始めに生じている」ということです。
「指定した日付になること」が期間計算の契機となり、その日付の開始時点は「午前０時」として正確に把握することができます。
したがって、その事実が生じた時点以後の最も近い端点（その日の午前０時）から期間計算を開始します。
例えば、消費税法第45条（課税資産の譲渡等及び特定課税仕入れについての確定申告）の「当該課税期間の末日の翌日から２月以内」というのは、課税期間の末日の翌日が４月１日である場合は、４月１日から起算して２か月を満了する６月30日までということになります。
経過する日・経過した日
期間の計算に関する用語で「経過する日」と「経過した日」という表現があります。
どちらも似たような表現なのでややこしいですが、意味はそれぞれ次のようになります。
例えば、2020年４月１日から「１年を経過する日」は、１年後の応当日の前日である2021年３月31日となり、2020年４月１日から「１年を経過した日」は、１年後の応当日である2021年４月１日となります。
どちらも同じ「１年」という期間を基準としているのに、なぜ指し示す日付が異なるのでしょうか？
これは、両者の指し示す期間の端点の取扱いが異なるからです。
「経過する」という表現を字義的に捉えると「現在進行形」の意味となり、その期間をまさに満了しようとするタイミングが期間の終わりになります。
しかし、１日の終わりを示す時刻は存在しないため、23時59分59.9999…秒と小数点以下が無限に続き翌日の午前０時に限りなく近づいていくタイミングがその期間の終わりになります。
この場合、例えば、「2020年４月１日から１年を経過する日まで」の示す期間をXとすると、Xは以下の時刻の範囲の期間として表すことができます。
2020年４月１日0:00 ≦ X ＜ 2021年４月１日0:00
一方、「経過した」という表現を字義的に捉えると「過去形」の意味となり、その期間をちょうど満了したタイミングになります。
１日を満了するタイミングは、翌日の午前０時として表すことができます。
例えば、「2020年４月１日から１年を経過した日まで」の示す期間をXとすると、Xは以下の時刻の範囲の期間として表すことができます。
2020年４月１日0:00 ≦ X ≦ 2021年４月１日0:00
したがって、「経過する日」は 「A ≦ X ＜ B」 という不等式表せる半開区間（左閉右開区間）の集合、「経過した日」は 「A ≦ X ≦ B」 という不等式で表せる閉区間の集合として捉えることができます。
これを踏まえて、「経過する日」と「経過した日」の示す期間について、フロアー関数のグラフで考えてみましょう。
「経過する日」の考え方
まず、「経過する日」について考える場合は、起算日の午前０時の端点（黒丸●）から、左側が黒丸●、右側が白丸○の棒を伸ばすイメージで考えます。
例えば、「４月１日から３日を経過する日」といった場合は、以下の期間で表すことができます。
４月１日0:00 ≦ X ＜ ４月４日0:00
これをグラフに当てはめてみると、午前０時の直前である23時59分59.9999…秒のタイミングを含む４月３日が「４月１日から３日を経過する日」となります。
「経過した日」の考え方
一方、「経過した日」について考える場合は、起算日の午前０時の端点（黒丸●）から、左側が黒丸●、右側も黒丸●の棒を伸ばすイメージで考えます。
例えば、「４月１日から３日を経過した日」といった場合は、は以下の期間で表すことができます。
４月１日0:00 ≦ X ≦ ４月４日0:00
これをグラフに当てはめてみると、不等式右辺の午前０時のタイミングを含む４月４日が「４月１日から３日を経過した日」となります。
国税に関する法律に別段の定めがあるとき
上述のとおり、期間の計算は原則として初日算入せず、午前０時から期間が開始する場合は初日算入することとされています。
しかし、法律で特別の定めがある場合は、上記の例によりません。
例えば、条文に「以前」「以後」「～日から起算して」という表現が含まれている場合は、基準となる時点を含む（初日算入する）こととなります。
一方、「前」「後」という表現が含まれている場合は、基準となる時点を含まない（初日不算入）こととなります。
前にさかのぼる場合の考え方
前に（過去に）さかのぼる場合の期間の考え方については、以下の記事の途中から自説を解説しています。よろしければこちらもご一読ください。
