前回の記事では、中間納付額の合計額から消費税額（国税分の中間納付額）と地方消費税額（中間納付譲渡割額）の内訳を求める計算式をご紹介しました。
今回は、なぜこのような計算式になるのかご説明したいと思います。
なお、計算式を導出するにあたっては、中高生レベルの数学的な考え方を使います。
また、この計算式は僕が独自に導いたものになります。公式として多くの人に活用されてほしいと思っています。
消費税の中間納付額の計算方法
消費税の中間納付額の計算は、一月中間申告、三月中間申告、六月中間申告の３種類の計算方法がありますが、今回はすでに納付済みの金額の内訳の計算が主題のため、それぞれの詳細な内容の説明は割愛します。
ただし、いずれの計算方法でも、最後に百円未満切捨てて税額を求めます。
この百円未満切捨を行うということが、計算式を導き出すうえでの一番ポイントになります。
地方消費税の中間納付譲渡割額の計算方法
地方消費税の中間納付譲渡割額は、国税である消費税の中間納付額に（地方税の税率/国税の税率）を乗じて、百円未満の金額を切捨てて計算します。
なお、（地方税の税率/国税の税率）については、税率５％の場合は1/4、税率８％の場合は17/63、税率10％の場合は22/78となります。
地方消費税の中間納付譲渡割の計算でも、百円未満切捨を行うことがポイントとなります。
中間納付額を数式で表現する
上記のとおり、消費税額も地方消費税額も「百円未満切捨」を行うことを踏まえて、中間納付額の合計額を数式で表現してみます。
ここで、ガウス記号を使って数式を立てます。
ガウス記号とは、以下のような性質を持つ関数で、床関数、フロアー関数、整数部分などと呼ばれることもあります。
ガウス記号
[ ]で表される関数。ある値を越えない最大の整数値を表す。X を実数，n を整数としたとき、n ≦ X ＜ n+1 ならば，[X]=n である。例えば，[2.34]=2，[-3.54]=-4。
ガウス記号を用いれば、小数点以下の端数を切り捨てた整数値となるため、これをうまく活用して消費税額と地方消費税額を表現します。
消費税額は百円未満を切り捨てて計算するため、中間納付消費税額の100分の1をＸと置いた場合、消費税（国税分）の納付額は以下の数式で表現できます。
また、地方消費税額は、消費税額（国税分）に（地方税の税率/国税の税率）を乗じて百円未満切捨を行うため、ガウス記号を用いて次のように表すことができます。
これを踏まえて、税率５％、８％、10％の場合のそれぞれの中間納付額の計算式を求めていきましょう。
税率10％の場合の計算式
中間納付額の合計額をＡ円とした場合、税率10％の場合の中間納付額は以下のように表せます。
これを[Ｘ]について解き、[Ｘ]＝ｎ（ｎ：整数）とおくと、次のようになります。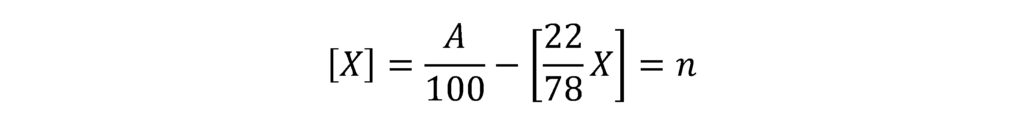 
ガウス記号を用いた関数の、以下の性質を用いて、Ｘの範囲を求めます。
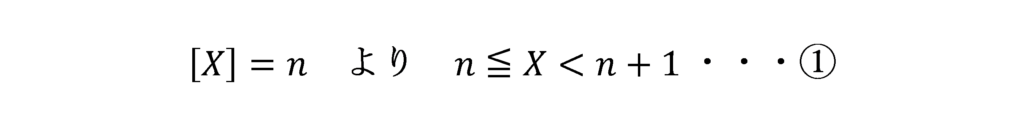
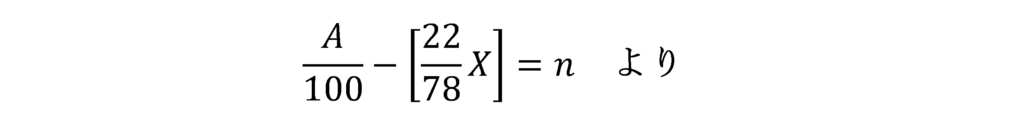
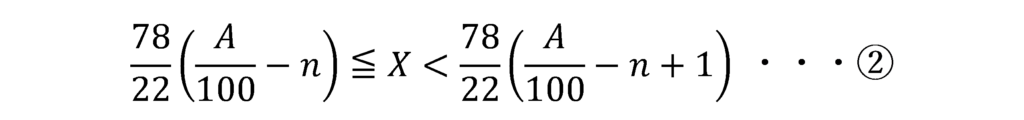
①と②を同時に満たすＸが存在するためのnの条件は以下のようになります。
これをｎについて解くと以下のようになります。
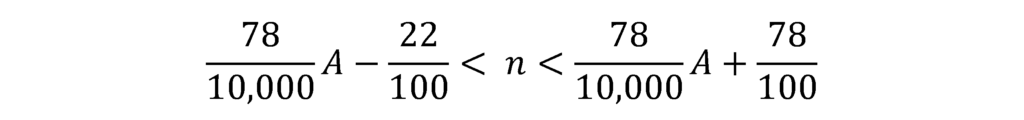
消費税額（国税分）＝100[X]=100ｎであるため、上記不等号の各辺に100を乗じると、消費税額（国税）の範囲が求まります。
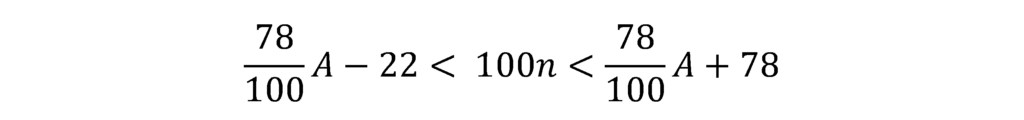
ｎは整数であることから、上記条件式の範囲内の100の倍数の金額が、中間納付した消費税額（国税分）の金額となります。
国税の消費税額が求められたら、地方消費税額は消費税額に22/78を乗じて、百円未満を切り捨てて求めます。
したがって、税率10％の場合の中間納付額の消費税額と地方消費税額の内訳は、次の算式で求めることができます。
税率８％の場合の計算式
中間納付額の合計額をＡ円とした場合、税率８％の場合の中間納付額は以下のように表せます。
これを[Ｘ]について解き、[Ｘ]＝ｎ（ｎ：整数）とおくと、次のようになります。
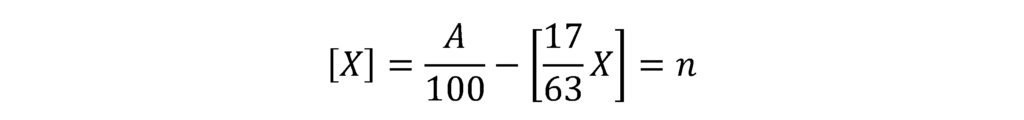
ガウス記号を用いた関数の、以下の性質を用いて、Ｘの範囲を求めます。
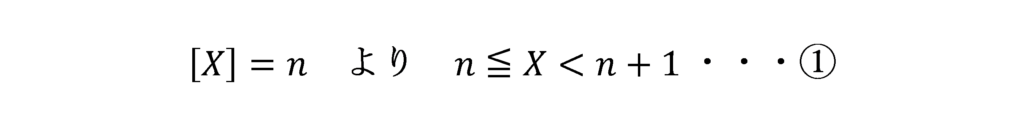
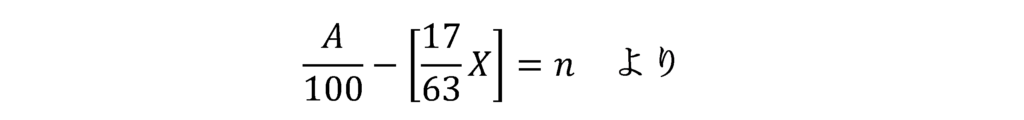
①と②を同時に満たすＸが存在するためのnの条件は以下のようになります。
これをｎについて解くと以下のようになります。
消費税額（国税分）＝100[X]=100ｎであるため、上記不等号の各辺に100を乗じると、消費税額（国税）の範囲が求まります。
ｎは整数であることから、上記条件式の範囲内の100の倍数の金額が、中間納付した消費税額（国税分）の金額となります。
国税の消費税額が求められたら、地方消費税額は消費税額に17/63を乗じて、百円未満を切り捨てて求めます。
したがって、税率８％の場合の中間納付額の消費税額と地方消費税額の内訳は、次の算式で求めることができます。
税率５％の場合の計算式
中間納付額の合計額をＡ円とした場合、税率５％の場合の中間納付額は以下のように表せます。
これを[Ｘ]について解き、[Ｘ]＝ｎ（ｎ：整数）とおくと、次のようになります。
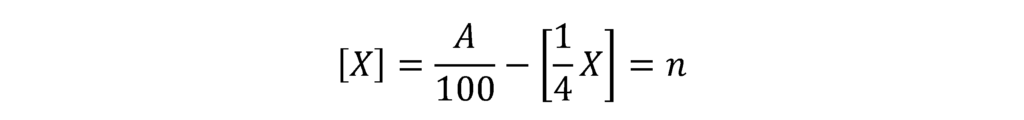
ガウス記号を用いた関数の、以下の性質を用いて、Ｘの範囲を求めます。
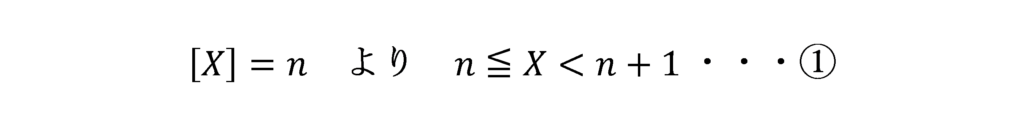
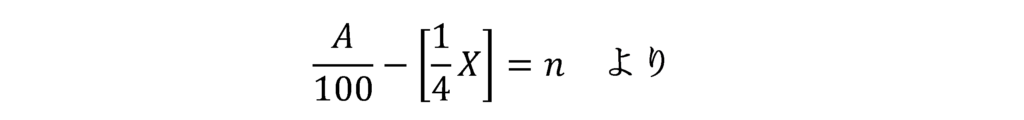
①と②を同時に満たすＸが存在するためのnの条件は以下のようになります。
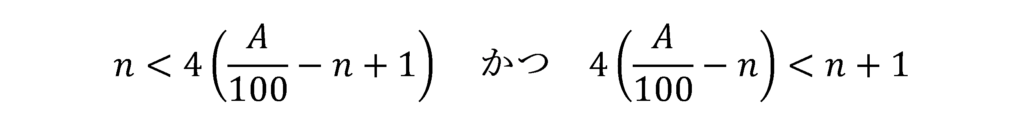
これをｎについて解くと以下のようになります。
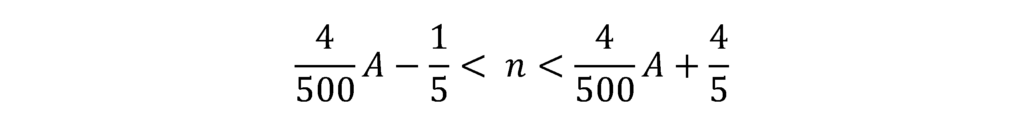
消費税額（国税分）＝100[X]=100ｎであるため、上記不等号の各辺に100を乗じると、消費税額（国税）の範囲が求まります。
ｎは整数であることから、上記条件式の範囲内の100の倍数の金額が、中間納付した消費税額（国税分）の金額となります。
国税の消費税額が求められたら、地方消費税額は消費税額に1/4を乗じて、百円未満を切り捨てて求めます。
したがって、税率５％の場合の中間納付額の消費税額と地方消費税額の内訳は、次の算式で求めることができます。
税率を一般化させた場合の計算式
最後に、税率をさらに一般化させ、国税の税率がα％、地方税の税率がβ％である場合の、中間納付額の国税と地方税の内訳を考えてみたいと思います。
この場合、地方消費税額は消費税額に（地方税の税率/国税の税率）を乗じて百円未満切捨して求めるため、以下のように表すことができます。
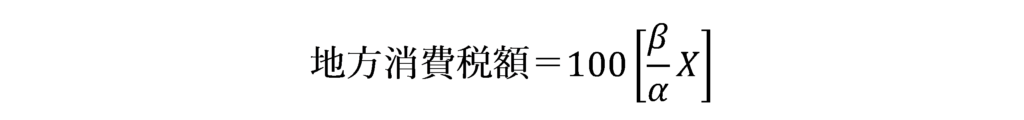
中間納付額の合計額をＡ円とした場合、税率（α＋β）％の場合の中間納付額は以下のように表せます。
これを[Ｘ]について解き、[Ｘ]＝ｎ（ｎ：整数）とおくと、次のようになります。
ガウス記号を用いた関数の、以下の性質を用いて、Ｘの範囲を求めます。
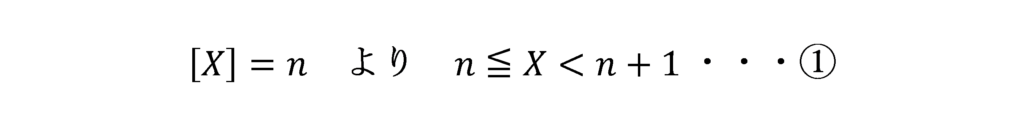
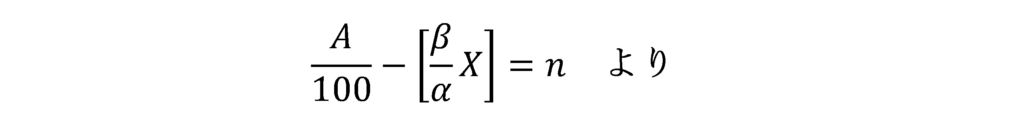
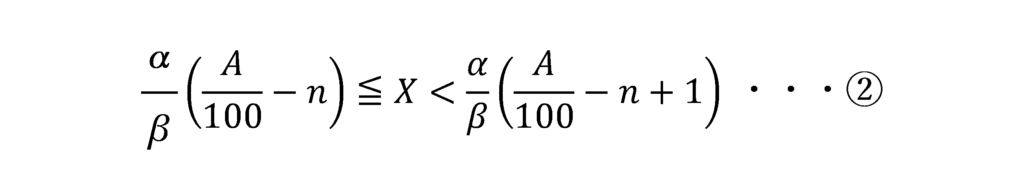
①と②を同時に満たすＸが存在するためのnの条件は以下のようになります。
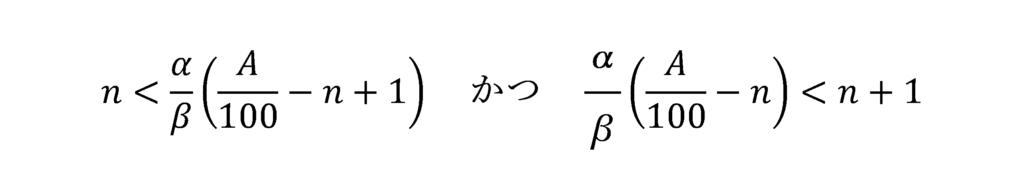
これをｎについて解くと以下のようになります。
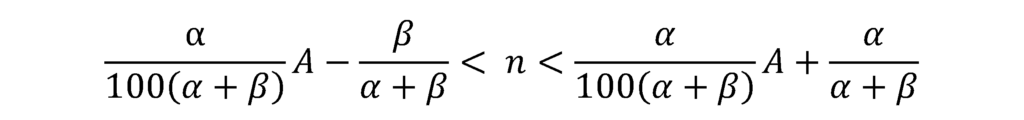
消費税額（国税分）＝100[X]=100ｎであるため、上記不等号の各辺に100を乗じると、消費税額（国税）の範囲が求まります。
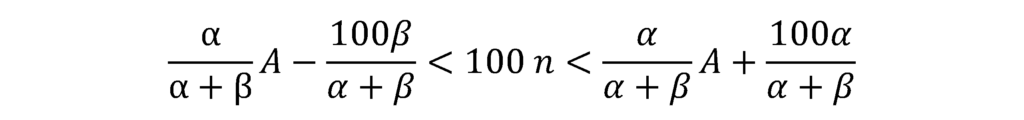
ｎは整数であることから、上記条件式の範囲内の100の倍数の金額が、中間納付した消費税額（国税分）の金額となります。
国税の消費税額が求められたら、地方消費税額は消費税額にβ/αを乗じて、百円未満を切り捨てて求めます。
したがって、税率（α＋β）％の場合の中間納付額の消費税額と地方消費税額の内訳は、次の算式で求めることができます。これで、将来もし税率が改正されても大丈夫です。
具体的な数値例を用いた計算方法は下記の記事で解説しています。
なお、中間納付額の金額によっては、この計算式で計算した結果、消費税額（国税分）と地方消費税額の合計が中間納付額と一致しない、または、消費税額（国税分）の金額が一意に定まらないなどの矛盾が起きることがあります。
「計算式が間違っているのでは？」と思うかもしれませんが、そうではありません。
それは、前提となるその中間納付額の金額そのものが誤っているからです。
この計算式が間違っているからではありません。
詳しくは、以下の記事をご覧ください。
